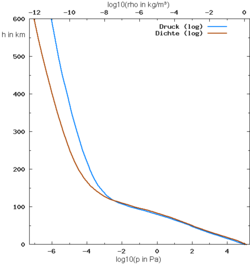
Zračni tlak in gostota zraka v odvisnosti od višine v ozračju (na grafu do 600 km)Zračni tlak kot funkcija višine nad morsko gladino (do 20 km) Barométrska enáčba opisuje pojemanje tlaka
p
{\displaystyle p\,}
višino
z
{\displaystyle z\,}
izotermnem ozračju :
p
(
z
)
=
p
0
e
−
z
/
z
0
.
{\displaystyle p(z)=p_{0}e^{-z/z_{0}}\!\,.}
V realnem ozračju se temperatura z višino spreminja, zato velja ta zveza le približno.
Izhaja se iz enačbe za hidrostatični tlak :
d
p
d
z
=
−
ρ
g
.
{\displaystyle {\frac {\mathrm {d} p}{\mathrm {d} z}}=-\rho g\!\,.}
Iz splošne plinske enačbe se lahko izrazi gostoto zraka
ρ
{\displaystyle \rho \,}
ρ
=
M
p
R
T
.
{\displaystyle \rho ={\frac {Mp}{RT}}\!\,.}
Ko se to vstavi v prejšnjo enačbo in preuredi, se dobi:
d
p
p
=
−
M
g
R
T
d
z
=
−
d
z
z
0
.
{\displaystyle {\frac {\mathrm {d} p}{p}}=-{\frac {Mg}{RT}}\,\mathrm {d} z=-{\frac {\mathrm {d} z}{z_{0}}}\!\,.}
Vpeljala se je oznaka
z
0
=
R
T
/
M
g
{\displaystyle z_{0}=RT/Mg\,}
integrira od
p
0
{\displaystyle p_{0}\,}
p
{\displaystyle p\,}
z
0
{\displaystyle z_{0}\,}
z
{\displaystyle z\,}
antilogaritmira , tako da se dobi:
p
=
p
0
e
−
z
/
z
0
.
{\displaystyle p=p_{0}e^{-z/z_{0}}\!\,.}
Izhaja se iz dejstva, da mora biti v ravnovesju kemijski potencial za vsako plast ozračja enak. V nasprotnem primeru bi neenakost kemijskih potencialov privedla do prenosa snovi med plastmi in porazdelitev snovi v ozračju ne bi bila ravnovesna.
Razliko kemijskih potencialov med izbrano referenčno ravnino (
z
=
0
{\displaystyle z=0\,}
temperaturi
T
{\displaystyle T\,}
μ
−
μ
0
=
H
¯
−
H
¯
0
+
R
T
ln
p
p
0
.
{\displaystyle \mu -\mu _{0}={\overline {H}}-{\overline {H}}_{0}+RT\ln {\frac {p}{p_{0}}}\!\,.}
Pri tem je
μ
{\displaystyle \mu \,}
μ
0
{\displaystyle \mu _{0}\,}
z
=
0
{\displaystyle z=0\,}
H
¯
{\displaystyle {\overline {H}}}
entalpija na mol in
H
¯
0
{\displaystyle {\overline {H}}_{0}}
z
=
0
{\displaystyle z=0\,}
p
{\displaystyle p\,}
tlak in
p
0
{\displaystyle p_{0}\,}
z
=
0
{\displaystyle z=0\,}
R
{\displaystyle R\,}
splošna plinska konstanta . Zadnji člen izvira iz izraza za spremembo entropije pri izotermni spremembi .
Brez izgube splošnosti se lahko postavi
H
¯
0
=
0
{\displaystyle {\overline {H}}_{0}=0\,}
z
{\displaystyle z\,}
težnostno potencialno energijo :
H
¯
=
M
g
z
.
{\displaystyle {\overline {H}}=Mgz\!\,.}
Pri tem je
M
{\displaystyle M\,}
molska masa plina ,
g
{\displaystyle g\,}
težni pospešek . Odtod se dobi zvezo:
M
g
z
=
−
R
T
ln
p
p
0
.
{\displaystyle Mgz=-RT\ln {\frac {p}{p_{0}}}\!\,.}
Če se jo antilogaritmira, se dobi izraz za pojemanje gostote z višino:
p
(
z
)
=
p
0
exp
(
−
M
g
z
R
T
)
.
{\displaystyle p(z)=p_{0}\exp \left(-{\frac {Mgz}{RT}}\right)\!\,.}
Izraz je identičen prej izpeljanemu, če se postavi
z
0
=
R
T
/
M
g
{\displaystyle z_{0}=RT/Mg\,}