Antične mezopotamske merske enote

Antične mezopotamske merske enote izvirajo iz ohlapno organiziranih mezopotamskih mestnih državic v zgodnjem sumerskem dinastičnem obdobju. Vsako mesto, kraljestvo in trgovski ceh je imelo svoje standarde vse do ustanovitve Akadskega kraljestva, ko jih je kralj Sargon poenotil. Standarde je izboljšal njegov vnuk, kralj Naram-Sin, po razpadu Akadskega kraljestva pa so se opustili. Naram-Sinove standarde so ponovno privzeli v obdobju Tretje urske dinastije in nepregledno množico različnih merskih enot zmanjšali na nekaj skladnih dogovorjenih skupin. Nasledniki sumerske civilizacije, vključno z Babilonci, Asirci in Perzijci, so sistem enot obdržali. Akadsko-sumersko meroslovje se je rekonstruiralo z uporabo statističnih metod, s katerimi so primerjali sumersko arhitekturo, arhitekturne načrte in objavljene uradne standarde kot sta kip Gudea B in bronasti nipurski komolec (vatel).
Arhaični sistem
[uredi | uredi kodo]
Merski sistemi, ki so kasneje postali klasični mezopotamski standardi, so se razvili vzporedno s pisavo v uruškem sumerskem obdobju okoli leta 4000 pr. n. .št.. Študije praklinopisa so pokazale, da se je v Uruku uporabljalo dvanajst različnih številčnih sistemov:
- šestdesetiški sistem S za štetje sužnjev, živali, rib, lesenih predmetov, kamnitih predmetov in posod
- šestdesetiški sistem S' za štetje mrtvih živali in določene vrste piva
- bi-šestdesetiški sistem B za računanje žita, kruha, rib in mlečnih proizvodov
- bi-šestdesetiški sistem B* za računanje obrokov
- GAN2 sistem G za računanje polj
- ŠE sistem Š za računanje volumna ječmena
- ŠE sistem Š' za računanje volumna slada
- ŠE sistem Š" za računanje volumna pšenice
- ŠE sistem Š* za računanje ječmenove kaše
- EN sistem E za računanje mase
- U4 sistem U za računanje koledarja
- DUGb sistem Db za računanje prostornine mleka
- DUGc sistem Db za računanje prostornine piva.
V zgodnjem sumerskem dinastičnem obdobju (okoli 2900-2300 pr. n. št.) se meroslovje in matematika nista ločevala in sta bili ena sama pisarska disciplina. Pojem abstraktnih števil še ni obstajal, zato so se vse količine zapisovale z meroslovnimi znaki in ne s števili, katerim je sledila oznaka enote. Znak za eno ovco, na primer, se je razlikoval od znaka za en dan, v nobenem pa ni bilo znaka za število ena. Arhaično sumersko meroslovje je zato zapleteno in ne povsem razumljivo.[1] Enote za dolžino, prostornino in maso so na splošno izhajale iz teoretičnega standardnega dela kocke, imenovanega gur, napolnjenega z ječmenom, pšenico, oljem ali vodo. Masa gura, imenovana gun2, je bila opredeljena kot masa, ki jo lahko nosi tovorni osel. Zaradi različnih gostot omenjenih dobrin in različnih številskih sistemov, šestdesetiškega in decimalnega, dimenzije kocke gur niso bile enotne. Različne kocke gur so temeljile na vodni kocki gur, korigirani z naslednjimi štirimi osnovnimi faktorji in njihovimi tretjimi koreni:
- Komma = 80/81, popravek pri načrtovanju obrokov za 360-dnevno leto
- Leimma = 24/25, za pretvarjanje iz decimalnega v šestdesetiški številski sistem
- Diesis = 15/16
- Euboic = 5/6
Eden od uradnih državnih standardov v arhaičnem sistemu je bil nipuski vatel (2650 pr. n. št.), ki je bil osnova za rekonstrukcijo merskega sistema.
Klasični sistem
[uredi | uredi kodo]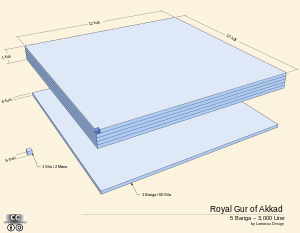
Sistem enot je temeljito reformiral akadski kralj Naram-Sin leta 2150 pr. n. št. Kralj je poenotil različne merske sisteme v en sam uradni standard, imenovan kraljevi gur.[2] Njegova reforma je pomenila prvi standardizirani sistem meril v Mezopotamiji. [2] Kraljevi gur (klinopisno: LU2.GAL.GUR, akadsko šarru kurru) je bil teoretični odsek kocke z dimenzijami 6 m 6 m x 0,5 m, napolnjen z vodo, iz katerega so se lahko izpeljale vse druge merske enote. Nansejevo pismo, ki ga je okoli leta 2000 pr. n. št. napisal kralj Gudea, kaže, da se je kraljevi gur uporabljal tudi v novosumerskem obdobju in zatem v Babilonskem, Asirskem in Perzijskem cesarstvu.
Dolžina
[uredi | uredi kodo]Enote za dolžino so imele predznak DU, ki je bil zapuščina arhaičnega merskega sistema, iz katerega so se razvile. Osnovne dolžinske enote so se uporabljala v arhitekturi in izmeri kmetijskih zemljišč.
| Osnovne dolžinske enote | ||||||
|---|---|---|---|---|---|---|
| Enota | Razmerje | Idealna vrednost | Sumersko | Akadsko | Klinopisno | |
| zrno | 1/180 | 0,0025 m | še | uţţatu | ||
| palec | 1/30 | 0,015 m | šu-si | ubānu | ||
| čevelj | 2/3 | 0,333 m | šu-du3-a | šīzu | ||
| vatel | 1 | 0,497 m | kuš3 | ammatu | ||
| korak | 2 | 1,000 m | ĝiri3 | šēpu | ||
| trs | 6 | 3,000 m | gi | qanû | ||
| palica | 12 | 6,000 m | nindan | nindanu | ||
| vrv | 120 | 60,000 m | eše2 | aslu | ||
Enote za razdaljo so bile, v nasprotju z enotami za dolžino, geodetske. Sumerska geodezija je zemljepisno širino med ekvatorjem in severnim polom razdelila na sedem con.
| Razdalja | ||||||
|---|---|---|---|---|---|---|
| Enota | Razmerje | Idealna vrednost | Sumersko | Akadsko | Klinopisno | |
| palica | 1/60 | 6,000 m | nidan | nindanu | ||
| vrv | 1/6 | 60,000 m | eše2 | aslu | ||
| kabel | 1 | 360 m | uš | uš | ||
| liga | 30 | 10.800 | da-na | bêru | ||
Ploščina
[uredi | uredi kodo]Merjenje ploščine se je razvilo iz računskega sistema GAN2 G. Posebna enota za število opek na enoto površine se je imenovala (klinopisno) sig.sar (sumersko šeg12-sar, akadsko libittu-mūšaru, slovensko opečni vrt) je štela 720 opek.
| Osnovne ploskovne enote | ||||||
|---|---|---|---|---|---|---|
| Enota | Razmerje | Dimenzije | Idealna vrednost | Sumersko | Akadsko | Klinopisno |
| šekel | 1/60 | 1kuš3 × 1kuš3 | 1 m² | gin2 | šiqlu | |
| vrt | 1 | 12kuš3 × 12kuš3 | 36 m² | sar | mūšaru | |
| četrt polja | 5 | 60kuš3 × 60kuš3 | 900 m² | uzalak | ? | |
| pol polja | 10 | 120kuš3 × 60kuš3 | 1,800 m² | upu | ubû | |
| polje | 100 | 60ĝiri3 × 60ĝiri3 | 3,600 m² | iku | ikû | |
| posestvo | 1800 | 3eše2 × 6eše2 | 64,800 m² | bur | būru | |
Prostornina
[uredi | uredi kodo]Prostornina se je merila po sistemu ŠE Š za suhe dobrine ali ŠE Š* za tekočine.
| Osnovne prostorske enote | ||||||
|---|---|---|---|---|---|---|
| Enota | Razmerje | Količina | Idealna vrednost | Sumersko | Akadsko | Klinopisno |
| šekel | 1/60 | 16,67 mL | 16,67 dm³ | gin2 | šiqlu | |
| skleda | 1 | 1 L | 0,001 m³ | sila3 | qû | |
| posoda | 10 | 10 L | 0,01 m³ | ban2 | sutū | |
| mernik | 60 | 60 L | 0,06 m³ | ba-ri2-ga | parsiktu | |
| gur | 300 | 300 L | 0,3 m³ | gur | kurru | |
Masa
[uredi | uredi kodo]
Masa se je tehtala s standardnimi utežmi. Za računanje se je uporabljal sistem EN E.
| Osnovne masne enote | ||||||
|---|---|---|---|---|---|---|
| Enota | Razmerje | Idealna vrednost | Sumersko | Akadsko | Klinopisno | |
| zrno | 1/180 | 0,05 g | še | uţţatu | ||
| šekel | 1 | 9 g | gin2 | šiqlu | ||
| funt | 60 | 497,7 g | ma-na | manû | ||
| tovor | 3.600 | 30.000 g | gun2 | biltu | ||
Čas
[uredi | uredi kodo]V arhaičnem sistemu se je čas meril po sistemu U4 U. V uporabi je bilo več lunisolarnih koledarjev. Babilonci so za svoj državni koledar privzeli koledar svetega mesta Nipur iz obdobja Tretje urske dinastije. [3] Nipurski koledar, ki je nastal okoli leta 3500 pr. n. št., je temeljil na še starejšem astronomskem znanju negotovega porekla. Glavni astronomski cikli, ki so se uporabili za izdelavo koledarja, so bili sinodski mesec, enakonočno leto in zvezdni dan.
| Basic Time | ||||||
|---|---|---|---|---|---|---|
| Enota | Razmerje | Idealna vrednost | Sumersko | Akadsko | Klinopisno | |
| geš | 1/360 | 240 s | mu-eš | geš | ||
| ura | 1/12 | 7.200 s | da-na | bêru | ||
| dan | 1 | 86.400 s | ud | immu | ||
| mesec | 30 | 2.592.000 s | itud | arhu | ||
| leto | 360 | 31.104.000 s | mu | šattu | ||
Povezava z drugimi meroslovji
[uredi | uredi kodo]Klasični mezopotamski merski sistem je bil osnova za elamitsko, hebrejsko, urartsko, huritsko, hetitsko, ugaritsko, feničansko, babilonsko, asirsko, perzijsko, arabsko in islamsko meroslovje.[4] Klasični mezopotamski sistem se je s trgovanjem delno prenesel tudi na bronastodobno harapsko in egipčansko metrologijo.
Sodobni Mednarodni sistem enot (SI) ne izhaja neposredno iz sumerskega meroslovje, vendar je od njega nasledil dogovor, da je sekunda 1/86400 sončevega dneva. Ena SI sekunda je zato enaka približno dvema sumerskima sekundama.
Sklici
[uredi | uredi kodo]- ↑ D.J. Melville (2006). Old Babylonian Weights and Measures. Pridobljeno 28. junija 2008.
- ↑ 2,0 2,1 M.A. Powell (1995). Metrology and Mathematics in Ancient Mesopotamia. V J.M. Sasson, Civilizations of the Ancient Near East III. New York, NY: Charles Scribner’s Sons. str. 3024. ISBN 0-684-19279-9.
- ↑ C.A. Ronan (2008). Measurement of time and types of calendars, standard units and cycles. Encyclopædia Britannica Online. Pridobljeno 28. junija 2008.
- ↑ C.R. Conder (1908). The Rise of Man. University of Michigan: J. Murray. str. 368.
