Darcyjev zakon

Darcyjev zakon je fizikalni zakon o sorazmernosti med specifičnim pretokom tekočine skozi porozno snov in hidravličnim gradientom v laminarnem režimu (majhno Reynoldsovo število ($\mathrm {Re} <10\!\,$)). Zakon je prvi formuliral Henry Darcy leta 1856 na podlagi rezultatov preskusov o pretoku vode skozi plasti peska in tvori osnovo hidrogeologije, veje geoznanosti.

$q={\frac {-k}{\eta }}\nabla p\!\,,$

kjer je:

• $q\!\,$ – hitrost pretoka tekočine $\left[\mathrm {m/s} \right]\!\,$,
• $k\!\,$ – prepustnost snovi $\left[\mathrm {m^{2}} \right]\!\,$,
• $\eta \!\,$ – dinamična viskoznost tekočine $\left[\mathrm {Pa\cdot s} \right]\!\,$,
• $\nabla p=\Delta p/L\!\,$ – hidravlični gradient – tlačna razlika, deljena z $L\!\,$ $\left[\mathrm {Pa/m} \right]\!\,$.

Zakon je soroden Ohmovemu zakonu iz elektrostatike in linearno povezuje hitrost prostorninskega pretoka tekočine z razliko hidravlične višine, ki je velikokrat sorazmerna s tlačno razliko, prek hidravlične prepustnosti.

Ozadje

Darcyjev zakon je prvi določil ekesperimentalno Darcy leta 1856, vendar se od tedaj izpeljuje iz Navier-Stokesovih enačb prek homogenizacijskih metod. Zakon je soroden s Poiseuillovim zakonom iz mehanike tekočin, Fourierovim zakonom s področja prevajanja toplote, Ohmovim zakonom s področja električnih tokokrogov in prvim Fickovim zakonom iz teorije difuzije.

Ena od uporab Darcyjevega zakona je analiza pretoka vode skozi vodonosnik – Darcyjev zakon se skupaj z zakonom o ohranitve mase poenostavi na enačbo pretoka podtalnice, eno od osnovnih zvez v hidrogeologiji.

Najprej je izboljšal Darcyjevo enačbo za enofazni tok Morris Muskat in v Darcyjevo enačbo enofazne (tekočinske) faze vključil viskoznost. Lahko se razume, da viskozne tekočine težje prehajajo skozi porozno snov kot manj viskozne tekočine. Zaradi te spremembe je bil zakon primeren za raziskovalce v naftni industriji. Na podlagi eksperimentalnih rezultatov njegovih kolegov Wyckoffa in Botseta sta Muskat in Meres naprej posplošila Darcyjev zakon, ki bi zajel večfazni tok vode, nafte in plina v porozni snovi nahajališča nafte. Splošne enačbe večfaznega toka Muskata in drugih zagotavljajo analitično osnovo za inženirstvo naftnih nahajališč, ki obstaja do danes.

Opis

Slika prikazuje definicijo in navodila za Darcyjev zakon. $A\!\,$ je površina prečnega preseka valja $\left[\mathrm {m^{2}} \right]\!\,$. $Q\!\,$ je hitrost pretoka $\left[\mathrm {m^{3}/s} \right]\!\,$ tekočine skozi površino $A\!\,$. Pretok tekočine skozi $A\!\,$ je $q=Q/A\!\,$. $L\!\,$ je višina valja. $\Delta p=p_{\rm {odtok}}-p_{\rm {dotok}}=p_{b}-p_{a}\!\,$. $\nabla p=\Delta p/L\!\,$ je hidravlični gradient med točkama $a\!\,$ in $b\!\,$.

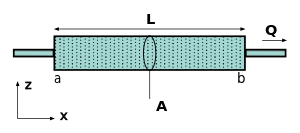
Darcyjev zakon, kakor ga je izboljšal Muskat, v odsotnosti gravitacijskih sil in v homogeni prepustni snovi, je dan s preprosto sorazmernostno zvezo med trenutnim prostorninskim tokom $q=Q/A\!\,$ (enote za $Q$: $\left[\mathrm {m^{3}/s} \right]\!\,$, enote za $A\!\,$: $\left[\mathrm {m^{2}} \right]\!\,$, enote za $q\!\,$: $\left[\mathrm {m/s} \right]\!\,$) skozi porozno snov, prepustnost snovi $k\!\,$, dinamična viskoznost tekočine $\eta \!\,$ in tlačna razlika $\Delta p\!\,$ na dani razdalji $L\!\,$, v obliki:

$q={\frac {-k}{\eta L}}\Delta p\!\,.$

Ta enačba za enofazni (tekočinski) pretok je definicijska enačba za absolutno prepustnost (enofazno prepustnost).

Glede na sliko na desni je pretok $q\!\,$ ali izpust na enoto površine določen v enotah $\left[\mathrm {m/s} \right]\!\,$, prepustnost $k\!\,$ v enotah $\left[\mathrm {m^{2}} \right]\!\,$, površina preseka $A\!\,$ v enotah $\left[\mathrm {m^{2}} \right]\!\,$, skupna tlačna razlika $\Delta p=p_{b}-p_{a}\!\,$ v enotah $\left[\mathrm {Pa} \right]\!\,$, dinamična viskoznost $\eta \!\,$ v enotah $\left[\mathrm {Pa\cdot s} \right]\!\,$ in $L\!\,$ je dolžina vzorca v enotah $\left[\mathrm {m} \right]\!\,$. Število teh parametrov je rabljeno v alternativnih definicijah spodaj. Negativni predznak se rabi v definiciji pretoka, ki sledi standardnemu dogovoru v fiziki, da tekočine tečejo iz območij z višjim tlakom v območja z nižjim tlakom. Pri tem je treba upoštevati hidravlično višino, če sta vstop in izstop na različnih višinah. Če je sprememba tlaka negativna, bo pretok v pozitivni smeri $x\!\,$. Obstaja več predlogov konstitutivne enačbe za absolutno prepustnost, najbolj znana pa je verjetno Kozenyjeva enačba (imenovana tudi Kozeny-Carmanova enačba).

Integralska oblika Darcyjevega zakona je dana kot:

$Q={\frac {-kA}{\eta L}}\,{\Delta p}\!\,,$

kjer je $Q\!\,$ (enote prostornina po času – $\left[\mathrm {m^{3}/s} \right]\!\,$) skupni iztok. Z upoštevanjem zveze za tlak statične tekočine (Stevinov zakon):

$p=\rho gh\!\,,$

se lahko Darcyjev zakon zapiše v obliki:

$Q={\frac {-kAg}{\nu L}}\,{\Delta h}\!\,,$

kjer je $\nu \!\,$ kinematična viskoznost z enoto $\left[\mathrm {m^{2}/s} \right]\!\,$. Odgovarjajoča hidravlična prevodnost je tako:

$K={\frac {k\rho g}{\eta }}={\frac {kg}{\nu }}\!\,$

z enoto $\left[\mathrm {m/s} \right]\!\,$ in Darcyjev zakon:

$q={\frac {-Kg}{L}}\Delta h\!\,.$

Količina $q\!\,$ ali $Q/A\!\,$, pogosto imenovana Darcyjev pretok ali Darcyjeva hitrost, ni hitrost, s katero tekočina potuje skozi pore. Hitrost pretoka $u\!\,$ je povezana s pretokom $q\!\,$ s poroznostjo $\varphi \!\,$ v obliki:

$u={\frac {q}{\varphi }}\!\,.$

Darcyjev zakon je preprosta matematična izjava in lepo povzema več znanih značilnosti podtalnice, ki teče v vodonosniku, vključno z:

• če na razdalji ni tlačnega gradienta, ne pride do pretoka (to so hidrostatične razmere),
• če obstaja tlačni gradient, bo pretok potekal od visokega proti nizkemu tlaku (nasprotno smeri naraščajočega gradienta – od tod negativni predznak v Darcyjevem zakonu),
• večji kot je tlačni gradient (skozi isto snov tvorbe), večja je stopnja praznjenja in
• hitrost izpusta tekočine bo pogosto različna – skozi različne snovi tvorbe (ali celo skozi isto snov, v drugi smeri) – tudi če v obeh primerih obstaja isti tlačni gradient.

Grafična ponazoritev uporabe enačbe pretoka podtalnice v ustaljenem stanju (temelji na Darcyjevem zakonu in ohranjanju mase) je pri izdelavi pretočnih mrež za kvantificiranje količine podtalnice, ki teče pod jezom.

Darcyjev zakon velja le za počasni, viskozni tok in večina primerov pretoka podtalnice spada v to kategorijo. Običajno je vsak tok z Reynoldsovim številom, manjšim od ena, očitno laminaren in zanj velja uporabiti Darcyjev zakon. Eksperimentalni testi so pokazali, da so lahko režimi pretoka z Reynoldsovim številom do 10 še vedno darcianski, kot v primeru toka podtalnice. Reynoldsovo število (brezrazsežni parameter) za pretok porozne snovi je običajno izraženo kot:

$\mathrm {Re} ={\frac {ud}{\nu }}\!\,,$

kjer je $\nu \!\,$ kinematična viskoznost vode, $u\!\,$ specifični izpust (in ne hitrost por – z enotami dolžine na čas), $d_{30}\!\,$ reprezentativni premer zrn za porozno snov (standardna izbira je d30, kar je 30 % velikost prehoda iz analize velikosti zrn z uporabo sit – z enotami za dolžino).

Izpeljava

Za stacionarni, plazeči, nestisljivi tok, tj. $\operatorname {d} (\rho u_{i})/\operatorname {d} t\approx 0\!\,$ se Navier-Stokesova enačba poenostavi v Stokesovo enačbo, ki je z zanemaritvijo skupnega člena enaka:

$\mu \nabla ^{2}u_{i}-\partial _{i}p=0\!\,,$

kjer je $\mu \!\,$ viskoznost, $u_{i}\!\,$ hitrost v smeri $i\!\,$ in $p\!\,$ tlak. Ob predpostavki, da je viskozna uporna sila linearna s hitrostjo, se lahko zapiše:

$-\left(k^{-1}\right)_{ij}\mu \varphi u_{j}-\partial _{i}p=0\!\,,$

kjer je $\varphi \!\,$ poroznost, $k_{ij}\!\,$ pa tenzor prepustnosti drugega reda. To da hitrost v smeri $n\!\,$:

$k_{ni}\left(k^{-1}\right)_{ij}u_{j}=\delta _{nj}u_{j}=u_{n}=-{\frac {k_{ni}}{\varphi \mu }}\partial _{i}p\!\,,$

kar da Darcyjev zakon za prostorninsko gostoto pretoka v smeri $n\!\,$:

$q_{n}=-{\frac {k_{ni}}{\mu }}\,\partial _{i}p\!\,.$

V izotropični porozni snovi so elementi zunaj diagonale v tenzorju prepustnosti enaki nič ($k_{ij}=0\!\,$ za $i\neq j\!\,$), elementi na diagonali so enaki $k_{ii}=k\!\,$, skupna oblika pa se pridobi kot spodaj, kar omogoča določitev hitrosti pretoka tekočine z reševanjem niza enačb v danem območju:

${\boldsymbol {q}}=-{\frac {k}{\mu }}\,{\boldsymbol {\nabla }}p\!\,.$

Zgornja enačba je vodilna enačba za pretok enofazne tekočine v porozni snovi.

Uporaba v naftnem inženirstvu

Druga izpeljava Darcyjevega zakona se obširno uporablja v naftnem inženirstvu za določanje pretoka skozi prepustne snovi — najpreprostejša od njih je za enorazsežno, homogeno kamninsko tvorbo z eno samo tekočo fazo in konstantno viskoznostjo tekočine.

Skoraj vsi naftni rezervoarji imajo vodno območje pod naftnim krakom, nekateri pa tudi plinski pokrov nad naftnim krakom. Ko tlak v rezervoarju pade zaradi pridobivanja nafte, teče voda v naftno cono od spodaj, plin pa v naftno cono od zgoraj (če obstaja plinski pokrov) in nastane sočasni tok in nemešljivo mešanje vseh tekočinskih faz v naftno cono. Upravljavec naftnega polja lahko tudi vbrizga vodo (in/ali plin), da izboljša proizvodnjo nafte. Naftna industrija zato uporablja posplošeno Darcyjevo enačbo za večfazni tok, ki so jo razvili Muskat in sodelavci. Ker je Darcyjevo ime tako razširjeno in močno povezano s tokom v poroznih snoveh, je večfazna enačba označena kot Darcyjev zakon za večfazni tok ali posplošena Darcyjeva enačba (ali zakon) ali preprosto Darcyjeva enačba (ali zakon) ali preprosto enačba toka, če kontekst pravi, da besedilo obravnava večfazno enačbo Muskata in sodelavcev. Večfazni tok v rezervoarjih nafte in plina je obsežna tema in eden od mnogih člankov o tej temi je Darcyjev zakon za večfazni tok.

Uporaba pri kuhanju kave

Številni dokumenti so uporabili Darcyjev zakon za modeliranje fizike kuhanja v loncu moka, natančneje, kako vroča voda pronica skozi zmleto kavo pod tlakom, najprej članek iz leta 2001, ki sta ga napisala Varlamov in Balestrino, nato članek iz leta 2007 Gianina, članek Navarinija in drugih iz leta 2008 ter članek Warrena D. Kinga iz leta 2008. V člankih so bodisi vzeli prepustnost kave kot konstantno kot poenostavitev ali pa so merili spremembe skozi postopek kuhanja.

Dodatne oblike zakona

Diferencialni izraz

Darcyjev zakon se lahko zelo na splošno izrazi kot:

$\mathbf {q} =-{\mathcal {K}}\nabla h\!\,,$

kjer je:

• $q\!\,$ – vektor prostorninskega pretoka tekočine v dani točki snovi,
• $h\!\,$ – skupna hidravlična višina,
• ${\mathcal {K}}\!\,$ – tenzor hidravlične prevodnosti v tej točki.

Hidravlična prevodnost se lahko velikokrat aproksimira kot skalar. (Pri tem je treba omeniti analogijo z Ohmovim zakonom v elektrostatiki. Vektor pretoka je analogen gostoti električnega toka, hidravlična višina je analogna električni napetosti, hidravlična prevodnost pa je analogna električni prevodnosti.)

Kvadratni zakon

Za pretoke v poroznih snoveh z Reynoldsovim številom, večjim od približno 1 do 10, lahko postanejo pomembni tudi vplivi vztrajn osti. Včasih se Darcyjevi enačbi doda vztrajnostni člen, znan kot Forchheimerjev člen. Ta izraz lahko pojasni nelinearno obnašanje podatkov o razliki tlaka v primerjavi s pretokom:

${\frac {\partial p}{\partial x}}=-{\frac {\mu }{k}}q-{\frac {\rho }{k_{1}}}q^{2}\!\,,$

kjer je dodatni člen $k_{1}\!\,$ znan kot vztrajnostna prepustnost.

Pretok v sredini rezervoarja peščenjaka je tako počasen, da Forchheimerjeva enačba običajno ni potrebna, toda pretok plina v vrtino za proizvodnjo plina je lahko dovolj visok, da upraviči uporabo Forchheimerjeve enačbe. V tem primeru izračuni zmogljivosti dotoka za vodnjak, ne mrežne celice 3D modela, temeljijo na Forchheimerjevi enačbi. Posledica tega je, da se v formuli učinkovitosti dotoka pojavi dodatna prevleka, odvisna od hitrosti.

Nekateri karbonatni rezervoarji imajo veliko razpok in Darcyjeva enačba za večfazni tok se posploši, da bi uravnavala tok v razpokah in tok v matriksu (tj. tradicionalni porozni kamnini). Neenakomerna površina sten prelomov in visok pretok v prelomih lahko upravičujeta uporabo Forchheimerjeve enačbe.

Popravek za pline v fini snovi (Knudsenova difuzija ali Klinkenbergov pojav)

Pri pretoku plina v majhnih značilnih dimenzijah (npr. zelo fin pesek, nanoporozne strukture itd.) postanejo interakcije delcev in stene pogostejše, kar povzroči dodatno trenje stene (Knudsenovo trenje). Za pretok v tem območju, kjer sta prisotna tako viskozno kot Knudsenovo trenje, je treba uporabiti novo formulacijo. Knudsen je predstavil polempirični model za pretok v prehodnem režimu, ki temelji na njegovih poskusih na majhnih kapilarah. Za porozno snov se lahko Knudsenova enačba zapiše kot:

$N=-\left({\frac {k}{\mu }}{\frac {p_{\mathrm {a} }+p_{\mathrm {b} }}{2}}+D_{\mathrm {K} }^{\mathrm {eff} }\right){\frac {1}{R_{\mathrm {g} }T}}{\frac {p_{\mathrm {b} }-p_{\mathrm {a} }}{L}}\!\,,$

kjer je $N\!\,$ molarni pretok, $R_{\mathrm {g} }\!\,$ plinska konstanta, $T\!\,$ temperatura, $D_{\mathrm {K} }^{\mathrm {eff} }\!\,$ efektivna Knudsenova difuznost porozne snovi. Model je mogoče izpeljati tudi iz binarnega modela trenja (BFM), ki temelji na prvem načelu. Diferencialna enačba prehodnega pretoka v porozni snovi, ki temelji na BFM, je podana kot:

${\frac {\partial p}{\partial x}}=-R_{\mathrm {g} }T\left({\frac {kp}{\mu }}+D_{\mathrm {K} }\right)^{-1}N\!\,.$

Ta enačba velja tako za kapilare kot za porozne snovi. Terminologija Knudsenov pojav in Knudsenova difuznost je pogostejša v strojništvu in kemijskem inženirstvu. V geološkem in petrokemičnem inženirstvu je ta pojav znan kot Klinkenbergov pojav. Z uporabo definicije molarnega pretoka se lahko zgornjo enačbo zapiše kot:

${\frac {\partial p}{\partial x}}=-R_{\mathrm {g} }T\left({\frac {kp}{\mu }}+D_{\mathrm {K} }\right)^{-1}{\dfrac {p}{R_{\mathrm {g} }T}}q\!\,.$

To enačbo se lahko preuredi v naslednjo obliko:

$q=-{\frac {k}{\mu }}\left(1+{\frac {D_{\mathrm {K} }\mu }{k}}{\frac {1}{p}}\right){\frac {\partial p}{\partial x}}\!\,.$

Če se primerja to enačbo z običajnim Darcyjevim zakonom, se lahko poda novo formulacijo kot:

$q=-{\frac {k^{\mathrm {eff} }}{\mu }}{\frac {\partial p}{\partial x}}\!\,,$

kjer je:

• $k^{\mathrm {eff} }=k\left(1+{\frac {D_{\mathrm {K} }\mu }{k}}{\frac {1}{p}}\right)\!\,.$

To je enakovredno formulaciji efektivne prepustnosti, ki jo je predlagal Klinkenberg:

$k^{\mathrm {eff} }=k\left(1+{\frac {b}{p}}\right)\!\,,$

kjer je $b\!\,$ znan kot Klinkenbergov parameter, odvisen od plina in strukture porozne snovi. To je dokaj jasno, če se primerja zgornje formulacije. Klinkenbergov parameter $b\!\,$ je odvisen od prepustnosti, Knudsenove difuznosti in viskoznosti (tj. značilnosti plina in porozne snovi).

Darcyjev zakon za kratke časovne lestvice

Za zelo kratke časovne lestvice se lahko Darcyjevemu zakonu doda časovni odvod pretoka, kar ima za posledico veljavne rešitve pri zelo majhnih časih (pri prenosu toplote se to imenuje spremenjena oblika (Fourierovega) zakona o prevajanju toplote):

$\tau {\frac {\partial q}{\partial t}}+q=-k\nabla h\!\,,$

kjer je $\tau \!\,$ zelo majhna časovna konstanta, zaradi katere se ta enačba zmanjša na normalno obliko Darcyjevega zakona v »normalnih« časih (večjih od nekaj nanosekund). Glavni razlog za to je, da pravilna enačba pretoka podtalnice (difuzijska enačba) vodi do singularnosti na konstantnih mejah hidravlične višine v zelo majhnih časih. Ta oblika je matematično strožja, vendar vodi do hiperbolične enačbe toka podtalnice, ki jo je težje rešiti in je uporabna le v zelo majhnih časih, običajno zunaj področja praktične uporabe.

Brinkmanova oblika zakona

Druga razširitev tradicionalne oblike Darcyjevega zakona je Brinkmanov člen, ki se uporablja za upoštevanje prehodnega pretoka med mejami. Uvedel ga je Henri Coenraad Brinkman leta 1949:

$-\beta \nabla ^{2}q+q=-{\frac {k}{\mu }}\nabla p\!\,,$

kjer je $\beta \!\,$ člen efektivne viskoznosti. Ta korekcijski člen upošteva pretok skozi snov, kjer so zrna snovi sama porozna, vendar jih je težko uporabljati in se običajno zanemarjajo.

Veljavnost zakona

Darcyjev zakon velja za laminarni tok skozi usedline. V drobnozrnatih usedlinah so razsežnosti vmesnih prostorov majhne, zato je tok laminaren. Tudi grobozrnate usedline se obnašajo podobno, vendar je v zelo grobozrnatih usedlinah lahko tok turbulenten. Zato Darcyjev zakon v takih usedlinah ne velja vedno. Za tok skozi komercialne krožne cevi je tok laminaren, ko je Reynoldsovo število manjše od 2000, in turbulenten, ko je večje od 4000, vendar je bilo v nekaterih usedlinah ugotovljeno, da je tok laminaren, ko je vrednost Reynoldsovega števila manjša od 1.

Glej tudi

• darcy – enota za prepustnost snovi
• hidrogeologija
• enačba pretoka podtalnice
• matematični model
• enačbe črnega olja

Viri

• Arora, K. R. (1989), Soil Mechanics and Foundation Engineering (2. izd.), Delhi: Standard Publishers Distributors, ISBN 81-8014-028-8
• Bejan, Adrian (1984), Convection Heat Transfer, John Wiley & Sons, doi:10.1002/9781118671627, ISBN 978-0-471-89612-8
• Brinkman, Henri Coenraad (1949), »A calculation of the viscous force exerted by a flowing fluid on a dense swarm of particles«, Applied Scientific Research, 1: 27–34, CiteSeerX 10.1.1.454.3769, doi:10.1007/BF02120313
• Carrigy, Nicholas B.; Pant, Lalit M.; Mitra, Sushanta Kumar; Secanell, Marc (2013), »Knudsen diffusivity and permeability of pemfc microporous coated gas diffusion layers for different polytetrafluoroethylene loadings«, Journal of the Electrochemical Society, 160 (2): F81–89, doi:10.1149/2.036302jes
• Cunningham, R. E.; Williams, R. J. J. (1980), Diffusion in Gases and Porous Media, New York: Plenum Press, doi:10.1007/978-1-4757-4983-0, ISBN 978-1-4757-4985-4
• Darcy, Henry (1856), Les fontaines publiques de la ville de Dijon, Pariz: Dalmont
• Gianino, Concetto (1. januar 2007), »Experimental analysis of the Italian coffee pot "moka"«, American Journal of Physics, 75 (1): 43–47, Bibcode:2007AmJPh..75...43G, doi:10.1119/1.2358157
• Jecl, Renata; Škerget, Leopold; Kramer, Janja (2005), »Primerjava med Forcheimerjevim in Brinkmanovim modelom konvektivnega toka v porozni kotanji z robnoobmočno integralsko metodo«, Acta hydrotechnica, [št.] 23 (38): 1–17, COBISS 256795648, ISSN 1581-0267
• Jin, Y.; Uth, M.-F.; Kuznetsov, A. V.; Herwig, H. (5. februar 2015), »Numerical investigation of the possibility of macroscopic turbulence in porous media: a direct numerical simulation study«, Journal of Fluid Mechanics, 766: 76–103, Bibcode:2015JFM...766...76J, doi:10.1017/jfm.2015.9, S2CID 119946306
• Kerkhof, Piet J. A. M. (1996), »A modified Maxwell–Stefan model for transport through inert membranes: The binary friction model«, Chemical Engineering Journal and the Biochemical Engineering Journal, 64 (3): 319–343, doi:10.1016/S0923-0467(96)03134-X
• King, Warren D. (1. junij 2008), »The physics of a stove-top espresso machine«, American Journal of Physics, 76 (6): 558–565, Bibcode:2008AmJPh..76..558K, doi:10.1119/1.2870524
• Klinkenberg, L. J. (1941), »The permeability of porous media to liquids and gases«, Drilling and Production Practice, Ameriški naftni inštitut, str. 200–213
• Liu, Mingchao; Suo, Si; Wu, Jian; Gan, Yixiang; Hanaor, Dorian A. H.; Chen, C. Q. (2019), »Tailoring Porous Media For Controllable Capillary Flow« (PDF), Journal of Colloid and Interface Science, 539: 379–387
• Nacionalna inženirska akademija (NAE) (2011), »Memorial Tributes: Volume 14«, NAP.edu (v angleščini), Washington, DC: The National Academies Press, doi:10.17226/12884, ISBN 978-0-309-15218-1
• Navarini, L.; Nobile, E.; Pinto, F.; Scheri, A.; Suggi-Liverani, F. (2009), »Experimental investigation of steam pressure coffee extraction in a stove-top coffee maker«, Applied Thermal Engineering, 29 (5–6): 998–1004, doi:10.1016/j.applthermaleng.2008.05.014
• Pant, Lalit M.; Mitra, Sushanta Kumar; Secanell, Marc (2012), »Absolute permeability and Knudsen diffusivity measurements in PEMFC gas diffusion layers and micro porous layers«, Journal of Power Sources, 206: 153–160, doi:10.1016/j.jpowsour.2012.01.099
• Varlamov, Andrij Andrijovič; Balestrino, Giuseppe (2001), »La fisica di un buon caffè«, Il Nuovo Saggiatore, 17 (3–4): 59–66
• Whitaker, Stephen (1986), »Flow in porous media I: A theoretical derivation of Darcy's law«, Transport in Porous Media, 1: 3–25, doi:10.1007/BF01036523, S2CID 121904058