De Moivreova fórmula [dé muávrova ~] (tudi Moivreova ~ ) je v matematiki formula , po kateri za vsako kompleksno število (in posebej za vsako realno število ) x in za vsako celo število n velja:
(
cos
x
+
i
sin
x
)
n
=
cos
(
n
x
)
+
i
sin
(
n
x
)
.
{\displaystyle \left(\cos x+i\sin x\right)^{n}=\cos \left(nx\right)+i\sin \left(nx\right)\!\,.}
Imenuje se po francoskem matematiku Abrahamu de Moivreu , Newtonovem prijatelju, ki jo je odkril leta 1707 in objavil leta 1722. Današnjo obliko ji je dal Leonhard Euler . Pomembna je zato, ker povezuje kompleksna števila (i je imaginarna enota ) in trigonometrične funkcije . Izraz
cos
x
+
i
sin
x
{\displaystyle \cos x+i\sin x\!\,}
včasih označijo kot
cis
x
.
{\displaystyle \operatorname {cis} \,x\!\,.}
Če razvijemo levo stran in primerjamo realne in imaginarne člene, lahko dobimo uporabne izraze za cos(nx ) in sin(nx ), izražene s cos(x ) in sin(x ). S formulo lahko najdemo eksplicitne izraze za n -te korene enote , oziroma kompleksna števila z , za katera velja zn = 1.
Čeprav je bila formula prej dokazana, se lahko preprosto izpelje iz Eulerjeve formule :
e
i
x
=
cos
x
+
i
sin
x
{\displaystyle e^{ix}=\cos x+i\sin x\!\,}
in pravil za množenje ali potenciranje eksponentne funkcije :
e
x
e
y
=
e
x
+
y
,
{\displaystyle e^{x}e^{y}=e^{x+y}\!\,,}
(
e
i
x
)
n
=
e
i
n
x
.
{\displaystyle \left(e^{ix}\right)^{n}=e^{inx}\!\,.}
Po Eulerjevi formuli potem sledi:
e
i
(
n
x
)
=
cos
(
n
x
)
+
i
sin
(
n
x
)
.
{\displaystyle e^{i(nx)}=\cos(nx)+i\sin(nx)\!\,.}
Obravnavamo tri primere.
Za n > 0 nadaljujemo s popolno indukcijo . Ko je n = 1, rezultat velja. Predpostavimo, da velja tudi za kakšen pozitivni celi k :
(
cos
x
+
i
sin
x
)
k
=
cos
(
k
x
)
+
i
sin
(
k
x
)
.
{\displaystyle \left(\cos x+i\sin x\right)^{k}=\cos \left(kx\right)+i\sin \left(kx\right)\!\,.}
Sedaj pogledamo primer za n = k + 1:
(
cos
x
+
i
sin
x
)
k
+
1
=
(
cos
x
+
i
sin
x
)
k
(
cos
x
+
i
sin
x
)
=
[
cos
(
k
x
)
+
i
sin
(
k
x
)
]
(
cos
x
+
i
sin
x
)
(po indukcijski predpostavki)
=
cos
(
k
x
)
cos
x
−
sin
(
k
x
)
sin
x
+
i
[
cos
(
k
x
)
sin
x
+
sin
(
k
x
)
cos
x
]
=
cos
[
(
k
+
1
)
x
]
+
i
sin
[
(
k
+
1
)
x
]
(
p
o
t
r
i
g
o
n
o
m
e
t
r
i
c
ˇ
n
i
h
e
n
a
k
o
s
t
i
h
)
{\displaystyle {\begin{alignedat}{2}\left(\cos x+i\sin x\right)^{k+1}&=\left(\cos x+i\sin x\right)^{k}\left(\cos x+i\sin x\right)\\&=\left[\cos \left(kx\right)+i\sin \left(kx\right)\right]\left(\cos x+i\sin x\right)\qquad {\mbox{(po indukcijski predpostavki)}}\\&=\cos \left(kx\right)\cos x-\sin \left(kx\right)\sin x+i\left[\cos \left(kx\right)\sin x+\sin \left(kx\right)\cos x\right]\\&=\cos \left[\left(k+1\right)x\right]+i\sin \left[\left(k+1\right)x\right]\qquad \mathrm {(po\,trigonometri{\check {c}}nih\,enakostih)} \end{alignedat}}}
Vidimo, da rezultat velja za n = k + 1, če velja za n = k . Po načelu popolne indukcije sledi, da rezultat velja za vsa pozitivna cela števila n ≥ 1.
Kadar je n = 0, formula velja, saj je
cos
(
0
x
)
+
i
sin
(
0
x
)
=
1
+
i
0
=
1
{\displaystyle \cos(0x)+i\sin(0x)=1+i0=1}
z
0
=
1
{\displaystyle z^{0}=1}
Za n < 0 obravnavamo takšen pozitivni celi m , da je n = −m . Tako je:
(
cos
x
+
i
sin
x
)
n
=
(
cos
x
+
i
sin
x
)
−
m
=
1
(
cos
x
+
i
sin
x
)
m
=
1
(
cos
m
x
+
i
sin
m
x
)
=
cos
(
m
x
)
−
i
sin
(
m
x
)
=
cos
(
−
m
x
)
+
i
sin
(
−
m
x
)
=
cos
(
n
x
)
+
i
sin
(
n
x
)
.
{\displaystyle {\begin{alignedat}{2}\left(\cos x+i\sin x\right)^{n}&=\left(\cos x+i\sin x\right)^{-m}\\&={\frac {1}{\left(\cos x+i\sin x\right)^{m}}}\\&={\frac {1}{\left(\cos mx+i\sin mx\right)}}\\&=\cos \left(mx\right)-i\sin \left(mx\right)\\&=\cos \left(-mx\right)+i\sin \left(-mx\right)\\&=\cos \left(nx\right)+i\sin \left(nx\right).\end{alignedat}}}
De Moivreov izrek tako velja za vse celoštevilske vrednosti n .
Formula velja tudi splošnejše: če sta
z
{\displaystyle z}
w
{\displaystyle w}
funkcija :
(
cos
z
+
i
sin
z
)
w
{\displaystyle \left(\cos z+i\sin z\right)^{w}\!\,}
zavzame več vrednosti, funkcija:
cos
(
w
z
)
+
i
sin
(
w
z
)
{\displaystyle \cos(wz)+i\sin(wz)\,}
pa ne. Vidimo, da je
cos
(
w
z
)
+
i
sin
(
w
z
)
{\displaystyle \cos(wz)+i\sin(wz)\,}
(
cos
z
+
i
sin
z
)
w
{\displaystyle \left(\cos z+i\sin z\right)^{w}\,}
Graf kubičnih korenov od 1 v kompleksni ravnini S formulo lahko najdemo n -te korene kompleksnega števila. Če je
z
{\displaystyle z}
z
=
r
(
cos
x
+
i
sin
x
)
,
{\displaystyle z=r\left(\cos x+i\sin x\right)\!\,,}
potem velja:
z
1
/
n
=
[
r
(
cos
x
+
i
sin
x
)
]
1
/
n
=
r
1
/
n
[
cos
(
x
+
2
k
π
n
)
+
i
sin
(
x
+
2
k
π
n
)
]
,
{\displaystyle {\begin{aligned}z^{1/n}&=\left[r\left(\cos x+i\sin x\right)\right]^{1/n}\\&=r^{1/n}\left[\cos \left({\frac {x+2k\pi }{n}}\right)+i\sin \left({\frac {x+2k\pi }{n}}\right)\right]\!\,,\end{aligned}}}
kjer je
k
{\displaystyle k}
n različnih korenov
z
{\displaystyle z}
k
{\displaystyle k}
0
{\displaystyle 0}
n
−
1
{\displaystyle n-1}
Abramowitz, Milton; Stegun, Irene A. (1964). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables . New York: Dover Publications. str. 74. ISBN 0-486-61272-4 §4.3.48 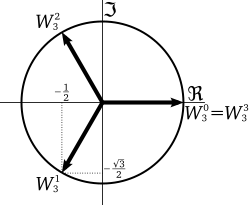









![{\displaystyle {\begin{alignedat}{2}\left(\cos x+i\sin x\right)^{k+1}&=\left(\cos x+i\sin x\right)^{k}\left(\cos x+i\sin x\right)\\&=\left[\cos \left(kx\right)+i\sin \left(kx\right)\right]\left(\cos x+i\sin x\right)\qquad {\mbox{(po indukcijski predpostavki)}}\\&=\cos \left(kx\right)\cos x-\sin \left(kx\right)\sin x+i\left[\cos \left(kx\right)\sin x+\sin \left(kx\right)\cos x\right]\\&=\cos \left[\left(k+1\right)x\right]+i\sin \left[\left(k+1\right)x\right]\qquad \mathrm {(po\,trigonometri{\check {c}}nih\,enakostih)} \end{alignedat}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/da82f9ecd3c282f07f60be89102812e1eadc5b54)









![{\displaystyle {\begin{aligned}z^{1/n}&=\left[r\left(\cos x+i\sin x\right)\right]^{1/n}\\&=r^{1/n}\left[\cos \left({\frac {x+2k\pi }{n}}\right)+i\sin \left({\frac {x+2k\pi }{n}}\right)\right]\!\,,\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/94800ec6f6059edb94fbeff0252da01fab34127e)


