Hermann–Mauguinova notacija

Hermann–Mauguinova notacija se uporablja v kristalografiji za opis elementov simetrij točkovnih, ploskovnih in prostorskih grup. Ime je dobila po nemškemu kristalografu Carlu Hermannu in francoskemu mineralogu Charles-Victorju Mauguinu. Notacija se včasih imenuje tudi mednarodna notacija.

Hermann–Mauguinova notacija ima v primerjavi s Schönfliesovo notacijo to prednost, ker se vanjo zlahka vključijo elementi translacjske simetrije in podrobno opišejo smeri osi simetrij.

Označevanje

Rotacijske simetrije se označujejo z n, ki je izračunan iz enačbe φ = 360º/n. φ je kot zasuka, po katerem ima kristal prvoten izgled. Zasuk za 180º je torej označen z n=2 in se imenuje 2-števna simetrija. n-ji se po dogovoru pišejo v padajočem zaporedju. Simetrijska os z največjim n je glavna os. Sledijo oznake dodatnih osi simetrije. Dvostranska simetrija, v kateri se po inverziji skozi točko in zasuku za kot φ=360º/n pojavi originalna slika, je označena z n. Najdaljša diagonala kocke je na primer označena s 3. Vse osi, ki se lahko izpeljejo iz drugih osi, se zanemarijo.

Vsaka os simetrije ima nič ali več zrcalnih ravnin, ki so z njo vzporedne ali pravokotne nanjo, se pravi, da jo sekajo. Zrcalne ravnine so označene z m. Primer: če kristalni razred vsebuje 4-števno os simetrije in zrcalno ravnino, ki je pravokotna nanjo, je označen s 4/m.

Kocka na primer ima tri 4-števne osi simetrije, ki gredo skozi središča ploskev, štiri 3-števne osi na telesnih diagonalah in šest 2-števnih osi, ki gredo skozi razpolovišča diagonalno nasprotnih robov. Ima tudi devet zrcalnih ravnin, od katerih so tri vzporedne s ploskvami, šest pa jih diagonalno seka ploskve. Ena od 4-števnih osi in ena od 3-števnih osi povsem zadostujeta za izpeljavo vseh ostalih 3- in 4-števnih osi. Na podoben način omogoča zrcalna ravnina, ki je pravokotna na 4-števno os, izpeljavo zrcalnih ravnin, ki sta vzporedni s ploskvami kocke. Iz ene od preostalih 2-števnih osi simetrije in nanjo pravokotne zrcalne ravnine se lahko izpelje še vse preostale 2-števne osi in zrcalne ravnine. Simetrija kocka bo torej opisana s 4/m 3 2/m.

Točkovne grupe

Točkovne grupe obstajajo v dvodimenzionalnem in trodimenzionalnem prostoru. Definirane so z elementi njihove simetrije, na primer z rotacijskimi in inverzijskimi osmi in zrcalnimi ravninami. Elementi translacijske simetrije, ki so prisotni v planarnih in prostorskih grupah, so izpuščeni. Nekateri elementi simetrije, ki se lahko izpeljejo iz drugih elementov, se lahko zaradi poenostavitve izpustijo.

V trodimenzionalnem prostoru je 32 kristalografskih točkovnih grup:

• 1, 1
• 2, m, ²⁄_m
• 222, mm2, mmm
• 4,4, ⁴⁄_m, 422, 4mm, 42m, ⁴⁄_mmm
• 3, 3, 32, 3m, 3m
• 6, 6, ⁶⁄_m, 622, 6mm, 62m, ⁶⁄_mmm
• 23, m3, 432, 43m, m3m

Ploskovne grupe

S Hermann-Mauguinovo notacijo se lahko opišejo tudi ploskovne grupe. Prva oznaka je mala črka p ali c, ki pomenita primitivno oziroma centrirano osnovno celico. Sledi oznaka rotacijske simetrije, tako kot v točkovnih grupah. Zrcalne ravnine so označene z m, drsno zrcaljenje pa z g.

Prostorske grupe

Prostorske grupe se lahko opišejo s kombinacijo identifikatorjev točkovnih grup in velikih črk, ki označujejo kristalno mrežo. Ko se k temu doda še translacije znotraj mreže, ki potekajo po vijačnih oseh in drsnih ravninah, je opis prostorske grupe popoln. Granat na primer je opisan z Ia3d.

Tipi kristalnih mrež

P primitivna v kubičnem kristalnem sistemu

I telesno centrirana v kubičnem kristalnem sistemu

F ploskovno centrirana v kubičnem kristalnem sistemu

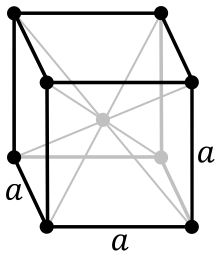
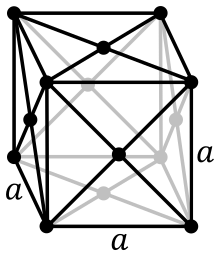
V prostoru so možne naslednje Bravaisove mreže:

• P primitivna
• I telesno centrirana (iz nemškega "Innenzentriert")
• F ploskovno centrirana (iz nemškega "Flächenzentriert")
• A vozli so samo na ploskvi A
• B vozli samo na ploskvi B
• C centriranje na a, b ali na ploskvi A, B
• R romboedrična

Vijačna os

Vijačna os je označena s številom n, ki je izračunano iz kota rotacije φ=360°/n. Številu se doda podpisani indeks, ki pove, za koliki del vzporednega mrežnega vektora je potekla translacija. Primera: oznaka 2₁ pomeni zasuk za 180° (dvoštevna rotacija), kateremu sledi translacija za ½ mrežnega vektorja; oznaka 3₁ pomeni zasuk ta 120° (trištevna rotacija), kateremu sledi translacija za ⅓ mrežnega vektorja.

Možne so naslednje vijačne osi: 2₁, 3₁, 4₁, 4₂, 6₁, 6₂ in 6₃.

Drsne ravnine

Drsne ravnine so označane s črkami a, b in c, odvisno od tega, vzdož katere osi je poteklo drseje. Možna sta tudi zdrsa n vzdolž polovice ploskovne diagonale in d vzdolž četrtine ploslovne diagonale ali telesne diagonale celice. Zdrs d se pogosto imenuje tudi drsna ravnina diamanta, ker se pojavlja v kristalni mreži diamanta.

Pomeni oznak:

• n_m pomeni n-števno vijačenje s tranlacijo za m,
• a, b ali c pomenijo drsno translacijo vzdolž polovice mrežnega vektorja te ploskve,
• n pomeni drsno translacijo vzdolž polovice ploskovne diagonale,
• d pomeni drsne ravnine s translacijo vzdolž četrtine ploskovne diadonale,
• e pomeni istočasni zdrs in translacijo vzdolž dveh različnih mrežnih vektorjev za polovico teh vektorjev.