Iz Wikipedije, proste enciklopedije
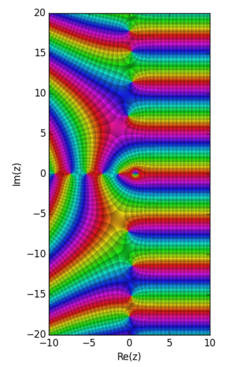 Barvna predstavitev Hurwitzeve funkcije
Barvna predstavitev Hurwitzeve funkcije  za
za  v kompleksni ravnini. Barva točke odkriva vrednost funkcije. Temnejše barve označujejo vrednosti blizu nič, odtenek pa argument vrednosti. Ustvarjena je s tiskalniško knjižnico matplotlib z različico metode domenskega barvanja.[1]
v kompleksni ravnini. Barva točke odkriva vrednost funkcije. Temnejše barve označujejo vrednosti blizu nič, odtenek pa argument vrednosti. Ustvarjena je s tiskalniško knjižnico matplotlib z različico metode domenskega barvanja.[1]
Hurwitzeva funkcija zeta (običajna označba  , včasih tudi
, včasih tudi  ) je v matematiki in še posebej v analitični teoriji števil ena od mnogih funkcij ζ. Imenuje se po nemškem matematiku Adolfu Hurwitzu.
) je v matematiki in še posebej v analitični teoriji števil ena od mnogih funkcij ζ. Imenuje se po nemškem matematiku Adolfu Hurwitzu.
Formalno je definirana za kompleksna argumenta  in
in  kot:
kot:

Ta neskončna vrsta je absolutno konvergentna za dane vrednosti  in
in  . Lahko se razširi na meromorfno funkcijo definirano za vse
. Lahko se razširi na meromorfno funkcijo definirano za vse  . Riemannova funkcija ζ je posebni primer za
. Riemannova funkcija ζ je posebni primer za  :
:

Funkcija trigama je posebni primer za  :
:













