Iz Wikipedije, proste enciklopedije
Kvadrik (tudi ploskev drugega reda ) je poljubna
n
{\displaystyle n\,}
hiperpovršina v
n
−
1
{\displaystyle n-1\,}
geometrijsko mesto ničel (korenov) kvadratnega polinoma .
Splošna oblika kvadrika je definirana z algebrsko enačbo :[ 1]
∑
i
,
j
=
1
n
+
1
x
i
Q
i
j
x
j
+
∑
i
=
1
n
+
1
P
i
x
i
+
R
=
0
,
{\displaystyle \sum _{i,j=1}^{n+1}x_{i}Q_{ij}x_{j}+\sum _{i=1}^{n+1}P_{i}x_{i}+R=0\!\,,}
kjer so:
{
x
1
,
x
2
,
…
,
x
n
+
1
}
{\displaystyle \{x_{1},x_{2},\ldots ,x_{n+1}\}\,}
Enačbo se lahko napiše s pomočjo vektorskega in matričnega zapisa:
x
Q
x
T
+
P
x
T
+
R
=
0
,
{\displaystyle xQx^{T}+Px^{T}+R=0\!\,,}
kjer je:
x
=
{
x
1
,
x
2
,
…
,
x
n
+
1
}
{\displaystyle x=\{x_{1},x_{2},\ldots ,x_{n+1}\}\,}
vrstični vektor
x
T
{\displaystyle x^{T}\,}
transponirana oblika vrstičnega vektorja
x
{\displaystyle x\,}
stolpični vektor )
Q
{\displaystyle Q\,}
matrika z razsežnostjo
(
n
+
1
)
×
(
n
+
1
)
{\displaystyle (n+1)\times (n+1)\,}
P
{\displaystyle P\,}
n
+
1
{\displaystyle n+1\,}
R
{\displaystyle R\,}
skalarna konstanta Kvadriki v evklidski ravnini imajo razsežnost
n
=
1
{\displaystyle n=1\,}
krivulje . Te vrste kvadriki so stožnice , ki se včasih imenujejo tudi koniki.
Elipsa (e =1/2) , parabola (e =1) in hiperbola (e =2) s stalnim goriščem F in vodilko (direkriso).V evklidskem prostoru imajo kvadriki razsežnost
n
=
2
{\displaystyle n=2\,}
kvadrične površine (površine drugega reda).
V naslednjem pregledu so prikazani izrojene (degenerirane) in neizrojene (nedegenerirane) kvadrične površine.
Nedegenerirane kvadrične površine
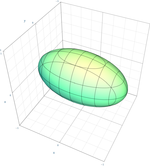
elipsoid
x
2
a
2
+
y
2
b
2
+
z
2
c
2
=
1
{\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}+{z^{2} \over c^{2}}=1\,}
sferoid (posebni primer elipsoida)
x
2
a
2
+
y
2
a
2
+
z
2
b
2
=
1
{\displaystyle {x^{2} \over a^{2}}+{y^{2} \over a^{2}}+{z^{2} \over b^{2}}=1\,}
sfera (posebni primer sferoida)
x
2
a
2
+
y
2
a
2
+
z
2
a
2
=
1
{\displaystyle {x^{2} \over a^{2}}+{y^{2} \over a^{2}}+{z^{2} \over a^{2}}=1\,}
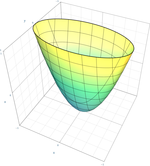
eliptični paraboloid
x
2
a
2
+
y
2
b
2
−
z
=
0
{\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}-z=0\,}
krožni paraboloid (posebni primer eliptičnega paraboloida)
x
2
a
2
+
y
2
a
2
−
z
=
0
{\displaystyle {x^{2} \over a^{2}}+{y^{2} \over a^{2}}-z=0\,}
hiperbolični paraboloid
x
2
a
2
−
y
2
b
2
−
z
=
0
{\displaystyle {x^{2} \over a^{2}}-{y^{2} \over b^{2}}-z=0\,}
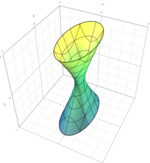
enodelni hiperboloid
x
2
a
2
+
y
2
b
2
−
z
2
c
2
=
1
{\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}-{z^{2} \over c^{2}}=1\,}
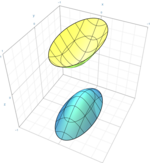
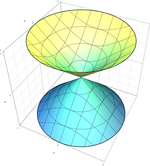
dvodelni hiperboloid
x
2
a
2
+
y
2
b
2
−
z
2
c
2
=
−
1
{\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}-{z^{2} \over c^{2}}=-1\,}
Degenerirane kvadrične površine
stožec
x
2
a
2
+
y
2
b
2
−
z
2
c
2
=
0
{\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}-{z^{2} \over c^{2}}=0\,}
krožni stožec (posebni primer stožca)
x
2
a
2
+
y
2
a
2
−
z
2
c
2
=
0
{\displaystyle {x^{2} \over a^{2}}+{y^{2} \over a^{2}}-{z^{2} \over c^{2}}=0\,}
eliptični valj
x
2
a
2
+
y
2
b
2
=
1
{\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}=1\,}
krožni valj (posebni primer eliptičnega valja)
x
2
a
2
+
y
2
a
2
=
1
{\displaystyle {x^{2} \over a^{2}}+{y^{2} \over a^{2}}=1\,}
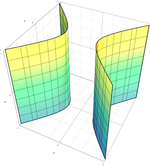
hiperbolični valj
x
2
a
2
−
y
2
b
2
=
1
{\displaystyle {x^{2} \over a^{2}}-{y^{2} \over b^{2}}=1\,}
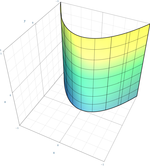
parabolični valj
x
2
+
2
a
y
=
0
{\displaystyle x^{2}+2ay=0\,}
Levy, Silvio (1995). »Quadrics« . Geometry Formulas and Facts, excerpted from 30th Edition of CRC Standard Mathematical Tables and Formulas (v angleščini). CRC Press, The Geometry Center, Univerza Minesote.