Mali zvezdni dodekaeder

Mali zvezdni dodekaeder
vrsta	Kepler-Poinsotov polieder
jedro stelacije	dodekaeder
elementi	F = 12, E = 30, V =12 ($\chi \,$ = -6)
stranskih ploskev na stranico	12 {5/2}
Schläflijev simbol	{5/2,5}
Wythoffov simbol	2 5/2
simetrijska grupa	Ih, H3, [5,3], *532
Coxeter-Dinkinov diagram
lastnosti	pravilni nekonveksni
(5/2)5 slika oglišč	veliki dodekaeder (dualni polieder)

Mali zvezdni dodekaeder je v Kepler-Poinsotov polieder. Ima Schläflijev simbol {5/2,5}. Je eden izmed štirih nekonveksnih pravilnih poliedrov. Sestavlja ga dvanajst pentagramskih stranskih ploskev, ki vsebujejo po pet pentagramov, ki se srečajo v vsakem oglišču.

Slike

Prosojni model	Ročno izdelani modeli
(glej tudi: animacijo)
sferno tlakovanje	stelacija	mreža telesa
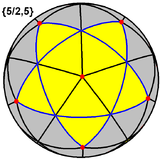Ta polieder predstavlja sferno tlakovanje z gostoto 3. (Ena petkotna stranska ploskev je prikazana v modri barvi in obarvana z rumeno)	Lahko jo konstruiramo kot prvo izmed treh stelacij dodekaedra in obravnavamo kot Wenningerjev model [W20].	Male stelirane dodekaedre lahko konstruiramo iz papirja ali lepenke tako, da povežemo 12 petstranih enakokrakih piramid na podoben način kot petkotnike v pravilnem dodekaedru. Z neprosojno snovjo se to kaže kot zunanji del vsake pentagramske stranske ploskve.

Sorodni poliedri

Konveksna ogrinjača je pravilni konveksni ikozaeder. Ta si deli svoje robove z velikim ikozaedrom.

Polieder je tudi prisekanje velikega dodekaedra:

Prisekani mali zvezdni dodekaeder izgleda na površni kot dodekaeder. Ima 24 stranskih ploskev.

ime	mali zvezdni dodekaeder	prisekani mali zvezdni dodekaeder	dodekadodekaeder	prisekani veliki dodekaeder	veliki dodekadodekaeder
Coxeter-Dinkinov diagram
Slika

Glej tudi

• sestav malega steliranega in velikega dodekaedra

Zunanje povezave

• Mali zvezdni dodekaeder na MathWorld (angleško)
• Stelacije dodekaedra na MathWorld (angleško)
• Uniformni poliedri (angleško)