Polni graf

Polni graf
K7, polni graf na 7-ih točkah
Točke	n
Povezave	n(n − 1) / 2
Premer	1
Notranji obseg	3 pri n ≥ 3
Avtomorfizem	n! (Sn)
Kromatično število	n
Kromatični indeks	n pri lihem n n-1 pri sodem n
Spekter	$\left\{{\begin{array}{ll}\{0^{1}\}&n=1\\\{(n-1)^{1},-1^{n-1}\}&{\text{drugače}}\end{array}}\right.$
Značilnosti	(n-1)-regularen simetričen točkovnoprehoden povezavnoprehoden z enotsko razdaljo krepkoregularen celoštevilski
Označba	$K_{n}\!\,$

Pólni gráf (redko tudi popólni gráf ali komplétni gráf) je v teoriji grafov graf, v katerem vsaka povezava povezuje par njegovih točk, oziroma kjer so vse točke povezane vsaka z vsako. Polni graf na n točkah se označuje s $K_{n}$. Število povezav je kot posledica leme o rokovanju enako trikotniškim številom (OEIS A000217):

Napaka pri razčlembi (SVG (MathML lahko omogočite z vtičnikom brskalnika): Neveljavni odziv (»Math extension cannot connect to Restbase.«) strežnika »http://localhost:6011/sl.wikipedia.org/v1/«:): {\displaystyle {n \choose 2} = \frac{n(n-1)}{2} \!\, . }

Polni graf je regularen stopnje n-1. Vsi polni grafi so maksimalno povezani, saj je točkovni prerez grafa, s katerim grafi postanejo nepovezani, kar celotna množica njegovih točk.

Polni graf z n točkami predstavlja robove $(n-1)\!\,$-simpleksa. Geometrijsko je K₃ soroden trikotniku, K₄ tetraedru, K₅ 5-celici (pentahoronu) ipd.

Ravninski graf ne more vsebovati subdivizije $K_{5}$ (ali polnega dvodelnega grafa $K_{3,3}$) kot podgrafa (izrek Kuratowskega). K₄ je torej največji polni graf, ki je še ravninski.

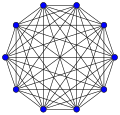
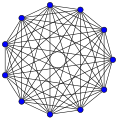
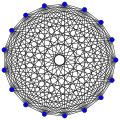
Polne grafe se običajno riše v obliki pravilnega mnogokotnika, razen grafa K₄. Polni grafi na n točkah pri n med 1 in 12 so prikazani spodaj s številom povezav:

• 
  K₁ (prazni graf N₁): 0
• 
  K₂: 1
• 
  K₃: 3
• 
  K₄: 6
• 
  K₅: 10
• 
  K₆: 15
• 
  K₇: 21
• 
  K₈: 28
• 
  K₉: 36
• 
  K₁₀: 45
• 
  K₁₁: 55
• 
  K₁₂: 66
• 
  K₁₃: 78
• 
  K₁₄: 91
• 
  K₁₅: 105
• 
  K₁₆: 120
• 
  K₁₇: 136
• 
  K₁₈: 153
• 
  K₁₉: 171
• 
  K₂₀: 190
• 
  K₂₁: 210
• 
  K₂₂: 231
• 
  K₂₃: 253
• 
  K₂₄: 276
• 
  K₂₅: 300

Glej tudi

• prazni graf
• pot

Zunanje povezave

• Weisstein, Eric Wolfgang. »Complete Graph«. MathWorld.