Protislovje
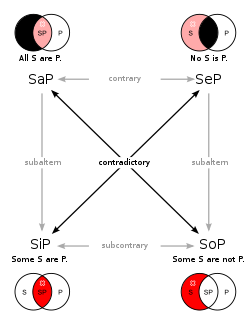
Protislóvje[1] (s tujko kontradíkcija[2][3]:607 in tudi antinomíja,[4][5]:55 starinsko protiréčje[6]) je v klasični logiki pojav ali stanje sestavljeno iz logične nezdružljivosti med dvema ali več trditvami (propozicijami). Pojavi se kadar dve trditvi vzeti skupaj vodita do dveh zaključkov (implikacij), ki tvorita logični, po navadi nasprotni inverziji drugega z drugim. Aristotelov zakon o neprotislovju ilustrira splošno težnjo v uporabni logiki in pravi, da je »nemogoče reči o nečem, da je in da ni v enakem oziru in v enakem času.«
Razširjeno gledano zunaj klasične logike se lahko govori o protislovjih med akcijami, kadar se predpostavi, da si njihovi vzroki med seboj nasprotujejo.
Zgodovina
[uredi | uredi kodo]S tvorjenjem paradoksa je Platonov dialog Evtidem prikazal potrebo po pojmu protislovja. V svojem dialogu je Dionisodor zanikal obstoj »protislovja,« Sokrat pa mu je nasprotoval:
- »Na svoje začudenje sem dejal: Kaj misliš Dionisodor? Velikokrat sem slišal in sem bil začuden, da sem slišal to tvojo tezo, ki jo vzdržujejo in rabijo Protagorovi učenci in mnogi pred njim. Zdi se mi dokaj presenetljiva in samomorilska kakor tudi uničujoča. Mislim, da sem verjetno o njeni resničnosti slišal od tebe. Izreka je, da ne obstaja nekaj kakor laž – človek mora reči kaj je resnično, drugače naj molči. Ali ni takšno tvoje mnenje?«
Dionisodor se je res strinjal, da »ne obstaja nekaj kot je napačno mnenje ... ne obstaja nekaj kar je nevednost« in je od Sokrata zahteval naj ga ovrže. Sokrat se je odzval: »Kako naj te ovržem, če, kakor praviš, je treba reči, da je laž nemogoča?«[7]
V formalni logiki
[uredi | uredi kodo]- Opomba: Simbol ⊥ (, falsum) predstavlja poljubno protislovje z dualom simbolom ⊤ (, verum), ki predstavlja poljubno tavtologijo. Protislovje se včasih označi kot »Opq«, tavtologija pa kot »Vpq«. Desno zasukani simbol ⊢ () po navadi pomeni »sledi« ali »je dokazano«.
V klasični logiki in še posebej v propozicijski logiki in logiki prvega reda je trditev protislovje, če in samo če je . Ker za protislovnost velja, da je za vse (ker je ), se lahko dokaže katerakoli trditev iz množice aksiomov, ki vsebuje protislovja. To se imenuje »načelo eksplozije« ali »ex falso quodlibet« (»iz laži sledi vse«).
V polni logiki je formula protislovna, če in samo če je nezadovoljiva.
Dokaz s protislovjem
[uredi | uredi kodo]Za trditev velja, da je , kar pomeni, da je tavtologija, oziroma, da je vedno resnična, če in samo če je , ali, če je negacija protislovje. Zato dokaz, da je tudi dokaže, da je resnična. Raba tega dejstva sestavlja tehniko dokaza s protislovjem, ki ga matematiki veliko rabijo. To velja le v logiki, ki kot aksiom rabi izključeni srednji .
Simbolična reprezentacija
[uredi | uredi kodo]V matematiki se simbol, ki predstavlja protislovje znotraj dokaza, razlikuje.[8] Nekateri simboli, ki se lahko rabijo za reprezentacijo protislovja, so: ↯, Opq, , ⊥, ↮ in ※. V vsakem simbolizmu se lahko protislovje zamenja za resničnostno vrednost »napačno,« ki ga simbolizira na primer znak »0.« Velikokrat se vidi okrajšava Q.E.D. ali kakšna različica takoj za simbolom protislovja – to se pojavi v dokazu s protislovjem, kjer se naznači, da je bila izvirna predpostavka napačna in, da mora biti njena negacija pravilna.
Pojem protislovja v aksiomatičnem sistemu in dokaz njegove neprotislovnosti
[uredi | uredi kodo]Dokaz o neprotislovnosti zahteva (i) aksiomatični sistem in (ii) prikaz, da se lahko formula p ter njena negacija ~p izpeljeta v njem. Vendar po katerikoli metodi se izpeljuje, bodo dokazi o neprotislovnosti izgledali kot da zahtevajo primitivni pojem protislovja – še več, izgleda, da bo ta pojem moral biti istočasno »zunaj« formalnega sistema v definiciji tavtologije.
Ko je Emil Leon Post v svojem delu iz leta 1921 Introduction to a general theory of elementary propositions razširil svoj dokaz neprotislovnosti propozicijske logike (to je logike) za tisto v delu Principia Mathematica (PM), je opazil, da v oziru na posplošeno množico postulatov (aksiomov) ni mogel več samodejno priklicati pojma »protislovja« – takšnega pojma postulati ne bi vsebovali:
- »Glavna zahteva za množico postulatov je, da je neprotislovna. Ker običajni pojem neprotislovnosti vključuje tisto o protislovju, ki spet vključuje negacijo, in ker se ta funkcija ne pojavlja v splošnem kot primitivna v [posplošeni množici postulatov], je potrebna nova definicija.«[9]
Postova rešitev problema je opisana v prikazu An Example of a Successful Absolute Proof of Consistency, ki sta ga podala Ernest Nagel in James Roy Newman in svojem delu Gödel's Proof iz leta 1958. Tudi onadva sta opazovala problem glede na pojem »protislovja« s svojima običajnima »pravilnostnima vrednostima« »pravilnosti« in »napačnosti.« Opazila sta, da je:
- »značilnost tavtologije definirana s pojmoma pravilnosti in napačnosti. Ta dva pojma očitno vključujeta sklic na nekaj zunaj formulskega računa. Zato postopek, omenjen v besedilu, v resnici ponuja interpretacijo računa z zagotovitvijo modela za sistem. Zaradi tega avtorji niso storili tega kar so obljubili, namreč definirati značilnost formul z izrazi čisto strukturnih gradnikov samih formul.« [Res] ... dokazi o neprotislovnosti, ki temeljijo na modelih, in, ki dokazujejo iz pravilnosti aksiomov na njihovo neprotislovnost, le spremenijo problem.«[10]
Z danimi nekaterimi »primitivnimi formulami«, kot sta primitiva iz PM S1 V S2 [inkluzivni ALI], ~S (negacija), je treba definirati aksiome v izrazih teh primitivnih pojmov. Vseskozi Post prikazuje v PM in definira (kakor tudi Nagel in Newman, glej spodaj), da je značilnost tavtologičnosti, ki jo je treba še definirati, »podedovana«: če se začne z množico tavtoloških aksiomov (postulatov) in dedukcijskim sistemom, ki vsebuje substitucijo in modus ponens, bo neprotislovni sistem dal le tavtološke formule.
Kaj bo torej definicija tavtologičnosti?
Nagel in Newman sta tvorila dva medsebojno izključujoča in izčrpljujoča se razreda K1 in K2 v katera pade (rezultat) aksiomov, kadar so njune spremenljivke, npr. S1 in S2, prirejene iz teh razredov. To velja tudi za primitivne formule. Na primer: »Formula z obliko S1 V S2 je dana v razred K2, če sta obe S1 and S2 v K2, drugače ja dana v K1« in »Formula z obliko ~S je dana v K2, če je S v K1, drugače je dana v K1.«[11]
Nagel in Newman sta lahko sedaj definirala pojem tavtologičnosti: »formula je tavtologija, če in samo če pade v razred K1 neglede v katerem od obeh razredov so postavljeni njeni elementi.«[12] Sedaj je značilnost »biti tavtologičen« opisana brez sklica na model ali interpretacijo.
- Če je na primer dana formula, kot je ~S1 V S2 in prireditev K1 v S1 in K2 v S2, se lahko ovrednoti in vstavi njen rezultat v enega od obeh razredov. Prireditev K1 v S1 postavi ~S1 v K2 – sedaj se lahko vidi, da ta prireditev povzroči, da formula pade v razred K2. Tako po definiciji ta formula ni tavtologija.
Post je opazil, da če je sistem protisloven, lahko dedukcija v njem (to je zadnja formula v zaporedju formul izpeljana iz tavtologij) končno prinese sámo S. Ker lahko prireditev spremenljivke S izhaja iz razreda K1 ali K2, dedukcija krši dedovalno značilnost tavtologije – izpeljava mora prinesti (ovrednotenje formule), ki bo padla v razred K1. Odtod je lahko Post izpeljal naslednjo definicijo protislovnosti brez rabe pojma protislovja:
- Deficija. Sistem bo protisloven, če prinese trditev nespremenjene spremenljivke p [S je v Newmanovih in Nagelovih zgledih].
Z drugimi besedami se lahko pojem »protislovja«razdeli kadar se konstruira dokaz neprotislovnosti – kar ga zamenja, je pojem »medsebojno izključujočih in izčrpljujočih se« razredov. Ni treba, da aksiomatični sistem, kar je še bolj zanimivo, nujno vsebuje pojem »protislovja.«
Filozofija
[uredi | uredi kodo]Pristaši epistemološke teorije koherentizma običajno trdijo, da je potreben pogoj za zagovor prepričanja v tem, da mora biti prepričanje del logičnega neprotislovnega sistema prepričanj. Nekateri diateleisti, kot tudi Grahan Priest, so razpravljali, da protislovje nujno ne zahteva neprotislovnosti.[13]
Pragmatična protislovja
[uredi | uredi kodo]Pragmatično protislovje se pojavi kadar vsak stavek argumenta nasprotuje trditvam, ki jih trdi. Neprotislovnost nastane v tem primeru, ker dejanje izraza namesto vsebine izrečenega izpodbija njegov zaključek.[14] Na primer verjetno Nietzschejeva izjava, da nekdo ne sme ubogati drugih, ali Mooreov paradoks. Znotraj analitične tradicije jih vidijo kot samoizpodbijajoče izjave in izvršna protislovja. Druge tradicije jih obravnavajo bolj kot zenovske koane v katerih avtorjevi nameni tvorijo protislovje s pomočjo tradicionalnega pomena, nato pa se sugerira nov pomen besede, ki ne nasprotuje izjavi.
Dialektični materializem
[uredi | uredi kodo]V dialektičnem materializmu se protislovja, kot so ipeljana iz hegeljanstva, po navadi nanašajo na nasprotstvo, ki neločljivo obstaja znotraj enega področja, ene poenotene sile ali objekta. To protislovje v nasprotju z metafizičnim mišljenjem ni objektivno nemogoča stvar, ker te protislovje sile obstajajo v objektivni stvarnosti in se med seboj ne izničujejo, ampak dejansko definirajo obstoj druga druge. Po marsistični teoriji se lahko takšna protislovja najde na primer v dejstvu, da:
- (a) velikansko bogastvo in produktivne moči soobstajajo skupaj
- (b) obstaja skrajna revščina in beda
- (c) obstaja (a), ki je v nasprotju z obstojem (b).
Hegeljanska in marksistična teorija določata, da bo dialektična narava zgodovine vodila do razveljavitve ali sinteze svojih protislovij. Marx je zato predpostavil, da bo zgodovina logično naredila, da se bo kapitalizem razvil v socialistično družbo, kjer bodo proizvodna sredstva enako služila izkoriščanemu in trpečemu družbenemu razredu in tako bo razrešeno predhodno protislovje med (a) in (b).[15]
Mao Cetungov filozofski esej O protislovju (《矛盾论》) iz leta 1937 je podprl Marxove in Leninove teze in predlagal, da je ves obstoj rezultat protislovja.[16]
Zunaj formalne logike
[uredi | uredi kodo]
Pogovorna raba lahko označuje akcije ali izjave, ki so si med seboj v naprotju, kadar so (ali so razumljene) kot posledica presupozicij, ki so protislovne v logičnem smislu.
Glej tudi
[uredi | uredi kodo]- antinomija
- Argument Clinic, skeč skupine Monty Python v katerem dva diskutanta pri svojem prerekanju rabita le ponavljajoča se protislovja
- nasprotnost
- dvojno merilo
- dvomiselnost
- ironija
- oksimoron
- parakonsistentna logika
- paradoks
- tavtologija
- TRIZ
Sklici
[uredi | uredi kodo]- ↑ »protislovje«. portal Fran 4.1. 25. maj 2017. Pridobljeno 25. julija 2017.
- ↑ »kontradikcija«. portal Fran 4.1. 25. maj 2017. Pridobljeno 25. julija 2017.
- ↑ Tavzes (2002), str. 607.
- ↑ »antinomija«. portal Fran 4.1. 25. maj 2017. Pridobljeno 25. julija 2017.
- ↑ Tavzes (2002), str. 55.
- ↑ »protirečje«. portal Fran 4.1. 25. maj 2017. Pridobljeno 25. julija 2017.
- ↑ Dialog Euthydemus iz The Dialogs of Plato v prevodu Benjamina Jowetta v: Knjiga 7 Plato: Robert Maynard Hutchins, glavni urednik, 1952, Great Books of the Western World, Enciklopedija Britannica, Inc., Chicago.
- ↑ Pakin (2017).
- ↑ Post (1921) v van Heijenoort (1967), str. 272.
- ↑ krepko in ležeče dodano, Nagel; Newman (1958), str. 109-110.
- ↑ Nagel; Newman (1958), str. 110-111.
- ↑ Nagel; Newman (1958), str. 111.
- ↑ Priest (2006).
- ↑ Stoljar (2006), str. 87.
- ↑ Sørensen (2006).
- ↑ Mao Cetung (1937).
Viri
[uredi | uredi kodo]- van Heijenoort, Jean (1967), From Frege to Gödel: A Source Book in Mathematical Logic 1879-1931, Cambridge, MA: Harvard University Press, ISBN 0-674-32449-8
- Mao Cetung (Avgust 1937), Selected Works of Mao Tse-tung: ON CONTRADICTION (v angleščini)
- Nagel, Ernest; Newman, James Roy (1958), Gödel's Proof, New York University Press, Card Catalog Number: 58-5610
- Pakin, Scott (19. januar 2017), The Comprehensive LaTeX Symbol List (PDF) (v angleščini), pridobljeno 26. julija 2017
- Priest, Graham (2006), In Contradiction: A Study of the Transconsistent (2. izd.), Oxford University Press, ISBN 0-19-926330-2
- Post, Emil Leon (1921), Introduction to a general theory of elementary propositions
- Sørensen, Michael Kuur (2006), CAPITAL AND LABOUR: CAN THE CONFLICT BE SOLVED? (v angleščini), pridobljeno 28. maja 2017
- Stoljar, Daniel (2006), Ignorance and Imagination, Oxford University Press - U.S., ISBN 0-19-530658-9
- Tavzes, Miloš, ur. (2002), Veliki slovar tujk, Ljubljana: Cankarjeva založba, COBISS 121003520, ISBN 961-231-271-0












