Coxeterjeva grupa
Coxeterjeva grupa je v matematiki abstraktna grupa, ki omogoča formalni opis grupe v okviru zrcalnih simetrij. Coxeterjeve grupe so končne evklidske zrcalne grupe. Kot zgled služijo simetrijske grupe pravilnih poliedrov. Coxeterjeve grupe so končne in ne morejo biti opisane s simetrijo in evklidskim zrcaljenjem.
Coxeterjeve grupe se veliko uporabljajo. Zgledi končnih Coxeterjevih grup vključujejo grupe simetrije pravilnih politopov in Weylovih grup enostavnih Liejevih algeber. Zgled neskončne Coxeterjeve grupe so tudi trikotniške grupe, ki odgovarjajo pravilni teselaciji evklidske in hiperbolične ravnine.
Grupe se imenujejo po angleško-kanadskem matematiku in geometru H. S. MacDonaldu Coxeterju (1907–2003).
Definicija
[uredi | uredi kodo]Coxeterjevo grupo se lahko definira kot grupo s predstavitvijo grupe kot:
kjer je:
- za
Pogoj pomeni, da se odnosa v obliki ne da prikazati.
Končne Coxeterjeve grupe
[uredi | uredi kodo]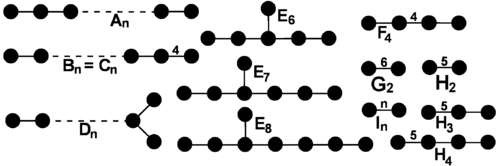
Razvrščanje
[uredi | uredi kodo]Končne Coxeterjeve grupe so razvrstili na osnovi Coxeter-Dinkinovih diagramov. Vse pa so predstavljene z zrcalnimi grupami končnorazsežnih evklidskih prostorov.
Končne Coxeterjeve grupe so sestavljene iz treh enoparameterskih družin z rastočim rangom , eno enoparametersko družino z razsežnostjo dva () in šestimi posebnimi grupami in .
Weylove grupe
[uredi | uredi kodo]Mnoge Coxeterjeve grupe, vendar ne vse, so Weylove grupe, vsaka Weylova grupa pa se lahko prikaže kot Coxeterjeva grupa. Weylove grupe sta družini in ter
Značilnosti
[uredi | uredi kodo]Nekatere značilnosti končnih Coxeterjevih grup so podane v naslednji preglednici:
| simbol grupe |
drugi simbol |
notacija z oklepaji | rank | red | sorodni politopi | Coxeter-Dinkinov diagram |
|---|---|---|---|---|---|---|
| An | An | [3n] | n | (n + 1)! | n-simpleks | |
| BCn | Cn | [4,3n-1] | n | 2n n! | n-hiperkocka / n-ortopleks | |
| Dn | Bn | [3n-3,1,1] | n | 2n−1 n! | n-polhiperkocka | |
| E6 | E6 | [32,2,1] | 6 | 72x6! = 51840 | 221, 122 | |
| E7 | E7 | [33,2,1] | 7 | 72x8! = 2903040 | 321, 231, 132 | |
| E8 | E8 | [34,2,1] | 8 | 192x10! = 696729600 | 421, 241, 142 | |
| F4 | F4 | [3,4,3] | 4 | 1152 | 24-celica | |
| G2 | - | [6] | 2 | 12 | šestkotnik | |
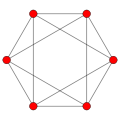
| H2 | G2 | [5] | 2 | 10 | petkotnik | |
| H3 | G3 | [3,5] | 3 | 120 | ikozaeder / dodekaeder | |
| H4 | G4 | [3,3,5] | 4 | 14400 | 120-celica / 600-celica | |
| I2(p) | D2p | [p] | 2 | 2p | p-kotnik |
Simetrijske grupe pravilnih politopov
[uredi | uredi kodo]Vse simetrijske grupe pravilnih politopov so končne Coxeterjeve grupe.
Znane so tri skupine pravilnih politopov v vseh mogočih razsežnostih. Simetrijska grupa pravilnega n-simpleksa je simetrijska grupa Sn+1, ki je znana tudi kot Coxeterjeva grupa tipa An. Simetrijska grupa n-kocke in njene dualne oblike n-ortopleksa je BCn, ki pa je znana kot hiperoktaederska grupa.
Posebni pravilni politopi v dveh, treh in štirih razsežnostih odgovarjajo drugim Coxeterjevim grupam. V dveh razsežnostih diedrske grupe, ki je grupa simetrije pravilnih mnogokotnikov, tvorijo skupino I2(p). V treh razsežnostih je simetrijska grupa pravilnih dodekaedrov in njihove dualne oblike ikozaedra je H3, ki je znana kot polna ikozaederska grupa. V štirih razsežnostih so znani trije posebni pravilni politopi. To so 24-celica, 120-celica in 600-celica.
Coxeterjeve grupe tipa Dn, E6, E7 in E8 so polpravilni politopi.
| grupa | An | BCn | Dn |
|
Hn | In(p) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 |  |
 |
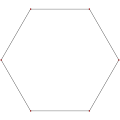 šestkotnik |
 petkotnik |
p-kotnik | ||||||||||
| 3 |  tetraeder |
 kocka |
 oktaeder |
 tetraeder |
 dodekaeder |
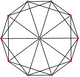 ikozaeder |
|||||||||
| 4 |  5-celica |
 |
 16-celica |
 |
 24-celica |
 120-celica |
 600-celica |
||||||||
| 5 |  5-simpleks |
 5-kocka |
 5-ortopleks |
 5-polkocka |
|||||||||||
| 6 |  6-simpleks |
 6-kocka |
 6-ortopleks |
 6-polkocka |
 122 |
 221 |
|||||||||
| 7 |  7-simpleks |
 7-kocka |
 7-ortopleks |
 7-polkocka |
 132 |
 231 |
 321 |
||||||||
| 8 |  8-simpleks |
 8-kocka |
 8-ortopleks |
 8-polkocka |
 142 |
 241 |
 421 |
||||||||
| 9 |  9-simpleks |
 9-kocka |
 9-ortopleks |
 9-polkocka |
|||||||||||
| 10 |  10-simpleks |
 10-kocka |
 10-ortopleks |
 10-polkocka |
|||||||||||
| družina n |
n-simpleks | n-hiperkocka | n-ortopleks | n-polkocka | 1k2 | 2k1 | k21 | ||||||||
Opomba:Oznake: An, Bn, Cn, Dn, Hn, E6, E7, E8, F4 in G2 so Coxeterjeva števila za posamezne Coxeterjeve grupe
Afine Coxeterjeve grupe
[uredi | uredi kodo]Afine Coxeterjeve grupe so druga pomembna skupina Coxeterjevih grup. To so tudi končne grupe, toda vsaka vsebuje normalno Abelovo podgrupo tako, da je faktorska grupa končna. Vsekakor pa je faktorska grupa Coxeterjeva grupa. Coxeterjev graf se dobi iz Coxeterjevega grafa Coxeterjeve grupe z dodajanjem novega vozlišča in dveh dodatnih povezav. V nadaljevanju so prikazane afine Coxeterjeve grupe.
| simbol grupe |
Wittov simbol |
notacija z oklepaji | sorodne uniformne teselacije | Coxeter-Dinkinov diagram |
|---|---|---|---|---|
| Pn+1 | [3[n+1]] | simplektično satovje :trikotno tlakovanje :tetraedersko-oktaedersko satovje |
||
| Sn+1 | [4,3n-2,31,1] | polkockino satovje | ||
| Rn+1 | [4,3n-1,4] | hiperkockino satovje | ||
| Qn+1 | [ 31,1,3n-3,31,1] | polhiperkubično satovje | ||
| T7 | [32,2,2] | 222 | ||
| T8 | [33,3,1] | 331, 133 | ||
| T9 | [35,2,1] | 521, 251, 152 | ||
| U5 | [3,4,3,3] | 16-cell satovje 24-celično satovje |
||
| V3 | [6,3] | šestkotno tlakovanje in trikotno tlakovanje |
||
| W2 | [∞] | apeirogon |
Zunanje povezave
[uredi | uredi kodo]- Weisstein, Eric Wolfgang. »CoxeterGroup«. MathWorld.
- Coxeterjeve grupe Arhivirano 2012-11-17 na Wayback Machine. (angleško)
























