Včrtana krožnica
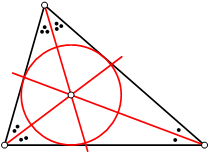
Včrtana krožnica je v ravninski geometriji krožnica, ki ima vse stranice danega mnogokotnika za tangente. Krog, ki ga omejuje ta krožnica, se imenuje včrtani krog.
Obstoj včrtane krožnice
[uredi | uredi kodo]Krožnico lahko včrtamo samo nekaterim mnogokotnikom. Takim mnogokotnikom rečemo tangentni mnogokotniki.
Če sta oba kraka danega kota tangenti neke krožnice, potem središče krožnice leži na simetrali kota. To nam omogoča konstrukcijo včrtane krožnice, pa tudi kriterij, kdaj včrtana krožnica sploh obstaja. Imejmo podan mnogokotnik:
- Najprej konstruiramo simetrale vseh notranjih kotov.
- Če se simetrale vseh kotov sekajo v isti točki, potem včrtana krožnica obstaja in ta točka je središče včrtane krožnice.
- Polmer včrtane krožnice je razdalja med središčem in poljubno stranico (merjeno pravokotno na to stranico).
Polmer včrtane krožnice je v novejših matematičnih učbenikih vedno označen z r, polmer očrtane krožnice pa z R (v starejših učbenikih je bil polmer včrtane krožnice ρ, polmer očrtane krožnice pa r).
Nekateri mnogokotniki, ki jim lahko zagotovo včrtamo krožnico:
Trikotniku včrtana krožnica
[uredi | uredi kodo]
Trikotnik ima značilnost, da se simetrale notranjih kotov vedno sekajo v isti točki, zato lahko trikotniku vedno včrtamo krožnico. Za polmer včrtane krožnice velja naslednja povezava s ploščino (p) trikotnika:
Pri tem je s polovični obseg (polobseg) trikotnika (enako kot pri Heronovi formuli):
Štirikotniku včrtana krožnica
[uredi | uredi kodo]Krožnico lahko včrtamo smo nekaterim štirikotnikom - imenujemo jih tangentni štirikotniki.
Karakteristična za tangentne štirikotnike je značilnost, da sta vsoti nasprotnih stranic enaki:
Za polmer včrtane krožnice velja podobna povezava s ploščino (p) kot pri trikotniku:
Pri tem je s polovični obseg štirikotnika:
Glej tudi
[uredi | uredi kodo]




