Trikotnik
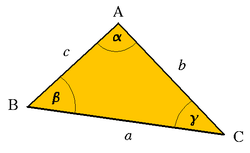
Trikotnik je eden osnovnih geometrijskih likov. Trikotnik je dvorazsežni lik s tremi oglišči in s tremi stranicami, ki so odseki treh premic. Običajno z izrazom trikotnik mislimo na ravninski lok. Na sferi govorimo npr. o sfernem trikotniku.
Vrste trikotnikov
[uredi | uredi kodo]Trikotnike lahko razdelimo glede na dolžine stranic. Tako imamo:
- enakostranični trikotnik: vse stranice so enako dolge. Enakostranični trikotnik je tudi enakokotni, saj so vsi trije notranji koti enaki 60°,
- enakokraki trikotnik: dve stranici sta enako dolgi. V enakokrakem trikotniku sta dva notranja kota enaka,
- enakokraki pravokotni trikotnik: dve stranici sta enako dolgi, notranji kot med njima pa je enak 90°.
- raznostranični trikotnik: vse tri stranice so različno dolge in vsi notranji koti različno veliki.
Trikotnike lahko razdelimo tudi glede na velikost največjega notranjega kota. Imamo:
- pravokotni trikotnik: en notranji kot je enak 90° (pravi kot). Stranica nasproti pravega kota je hipotenuza in je najdaljša stranica v trikotniku. Drugi dve stranici sta kateti,
- topokotni trikotnik: en notranji kot je večji od 90° (topi kot),
- ostrokotni trikotnik: vsi notranji koti so manjši od 90° (ostri koti).
notranji koti skupaj merijo 180˙zunanji koti pa merijo skupaj 360˙
Višina
[uredi | uredi kodo]Višina na stranico je oddaljenost oglišča od nosilke nasprotne stranice.
Obseg
[uredi | uredi kodo]Obseg je skupna dolžina vseh treh stranic:
V nekaterih zvezah se uporablja tudi polovični obseg (polobseg), ki je označen s črko s:
Ploščina
[uredi | uredi kodo]Ploščina trikotnika je enaka polovični ploščini paralelograma, katerega nevzporedni stranici sta dve od trikotnikovih stranic.
Lahko jo izračunamo tudi s Heronovo enačbo:
Če poznamo vse tri notranje kote ali vse tri stranice ter polmer včrtane ali očrtane krožnice (gl. enega nadaljnjih razdelkov), jo lahko izračunamo kot:
Če so koordinate točk A, B in C v pravokotnem koordinatnem sistemu enake , in , se ploščina izračuna kot:
Negativna vrednost izraza pod absolutno vrednostjo pomeni, da je usmerjenost trikotnika negativna.
Usmerjenost trikotnika
[uredi | uredi kodo]Če si oglišča A, B in C v tem zaporedju sledijo v smeri, ki je nasprotna smeri urinega kazalca, je trikotnik pozitivno usmerjen, v nasprotnem primeru je usmerjen negativno.
Notranji koti
[uredi | uredi kodo]V vsakem ravninskem trikotniku je vsota notranjih kotov enaka iztegnjenemu kotu:
Trikotniška neenakost
[uredi | uredi kodo]V vsakem neizrojenem ravninskem trikotniku velja trikotniška neenakost, ki pravi, da je vsota dolžin katerihkoli dveh stranic večja od dolžine tretje stranice. Torej:
Tri posebne točke trikotnika
[uredi | uredi kodo]
Trikotnik ima tri klasične posebne točke:
- središče očrtane krožnice (na zgornji sliki modre barve) je v sečišču simetral vseh treh stranic. Očrtana krožnica vsebuje vsa tri oglišča
- središče včrtane krožnice (na zgornji sliki rdeče barve) je v sečišču simetral vseh treh kotov. Včrtana krožnica se dotika vseh treh stranic, vendar jih ne seka
- težišče (tudi centroid) (na zgornji sliki zelene barve) je v sečišču premic, ki povezujejo oglišča z razpolovišči nasprotnih stranic.
Polmer očrtane in včrtane krožnice
[uredi | uredi kodo]Polmer očrtane krožnice lahko izračunamo tako:
Polmer včrtane krožnice pa tako:
Za razdaljo d med središčema očrtane in vrčrtane krožnice velja Eulerjeva trikotniška enačba:
Druge točke trikotnika
[uredi | uredi kodo]Višinska točka je v sečišču višin vseh treh stranic.
Razpolovišča stranic in končne točke višin ležijo na krožnici, ki se imenuje krožnica devetih točk ali Eulerjeva krožnica. Njen polmer je enak polovici polmera očrtane krožnice in se dotika včrtane krožnice v Feuerbachovi točki in treh zunanjih krožnic.
Težišče, središče očrtane krožnice, višinska točka in središče krožnice devetih točk so kolinearne in ležijo na Eulerjevi premici. Središče krožnice devetih točk leži na polovici med središčem včrtane in očrtane krožnice. Razdalja med težiščem T in središčem očrtane krožnice je enaka polovici razdalje med težiščem in višinsko točko V in velja:
Izreki v trikotniku
[uredi | uredi kodo]Zveze med stranicami in koti urejajo naslednji izreki:
Drugi izreki v zvezi s trikotniki:
- trikotnik in prečnica:
- Menelajev izrek (poznal ga je že Evklid)
Zunanje povezave
[uredi | uredi kodo]





















