Devetinpetdeset ikozaedrov

Devetinpetdeset ikozaedrov je knjiga, ki so je napisali in ilustrirali Coxeter (1907-2003) in Du Val (1903-1987), V. T. Flather in Petrie. Oštevilčili so večje število stelacij pravilnih konveksnih ali platonskih ikozaedrov v skladu s pravili, ki jih je postavil Miller.

Najprej je bila izdana na Univerzi v Torontu v letu 1938, drugo izdajo je pripravil Springer-Verlag v letu 1982. K. In D. Crennell sta obnovila besedilo in ponovno narisala diagrame za Tarqiunovo tretjo izdajo v letu 1999. Dodala sta še nekaj snovi in fotografij.

Prispevki avtorjev

Millerjeva pravila

Čeprav Miller (1906-1981) ni neposredno prispeval h knjigi, je bil močan prijatelj Coxeterja in Petrieja. Njegov prispevek je postal nesmrten s skupino pravil za definicijo oblik stelacije in se jih lahko obravnava kot »posebno pomembne:«

(i) Stranske ploskve morajo ležati v dvanajstih ravninah, to pa so povezovalne ravnine pravilnega ikozaedra.

(ii) Vsi deli, ki sestavljajo stranske ploskve morajo biti v isti ravnini, čeprav so nepovezani.

(iii) Vsi deli, ki so vključeni v eno ravnino morajo imeti trigonalno simetrijo brez ali z zrcaljenja. To zagotavlja ikozaedersko simetrijo celega telesa.

(iv) Vsi iz ene ravnine morajo biti »dosegljivi« v celotnem telesu (to pa pomeni, da morajo biti »zunanji.« V nekaterih primerih to zahteva ogromne modele, da bi se videla celotna zunanjost. Z modeli običajne velikosti so nekateri deli »zunaj.«

(v) Ne obravnavamo pa primerov, kjer lahko dele delimo v dve skupini, ki dasta telesu, lastnost, da ima vsak del toliko simetrije kot celotno telo. Dovolimo pa kombinacijo enenciomorfnih parov, ki nimajo skupnega dela, kar se pojavlja samo v enem primeru.

Pravila (I) do (III) so zahteve po simetriji za ravnine stranskih ploskev. Pravilo (IV) izključuje zakopane skrite luknje, tako, da nobeni dve stelaciji na zunaj ne izgledata enako. Pravilo (V) preprečuje, da bi nastali poljubni nepovezani sestavi enostavnejših stelacij.

Coxeter

Coxeter je bil glavna gonilna sila pri svojem delu. Izdelal je analizo Millerjevih pravil in pri tem uporabil večje število tehnik, kot so kombinatorika in abstraktna teorija grafov. Uporaba teh tehnik v geometrijskem okolju je bila takrat novost.

Opazil je, da diagrami stelacije uporabljajo mnoge segmente premic. Razvil je postopek za delo s kombinacijo sosednjih področij ravnin. Pri tem je oštevilčil dovoljene kombinacije, ki jih dovoljujejo Millerjeva pravila.

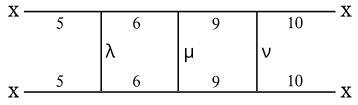
Njegova slika, ki je prikazana tukaj, prikazuje različne stranske ploskve, ki jih najdemo v diagramu stelacije (glej spodaj). Grški simboli predstavljajo množico možnih alternativ:

λ je lahko 3 ali 4

μ je lahko 7 ali 8

ν je lahko 11 ali 12

Du Val

Du Val je prispeval simbolično označevanje za določanje množice skladnih celic, ki so osnovane na opažanjih, da ležijo v »lupinah« okrog prvotnega ikozaedra. Na osnovi tega je preizkusil vse možne kombinacije Millerjevih pravil in s tem je potrdil Coxeterjev bolj analitični pristop.

Flather

Flatherjev prispevek je bil bolj posreden. Pripravil je modele vseh devetinpetdesetih ikozaedrov. Ko je prvič srečal Coxeterja je že izdelal mnoge stelacije vključno z neMillerjevimi primeri. Dodal je še popolno skupino devetinpetdesetih ikozaedrov, ki so bili ohranjeni v matematični knjižnici Univerze v Cambridgu na Angleškem. Knjižnica je imela tudi nekaj neMillerjevih modelov, toda ni jasno kateri od njih je naredil Flather in katere Millerjevi študentje ^[1].

Petrie

John Flinders Petrie je bil dolgoletni Coxetrov prijatelj. Tako je imel možnost spoznati štirirazsežno geometrijo. On in Coxeter sta delala skupaj na mnogih metematičnih problemih. Njegov prispevek k devetinpetdesetim ikozaedrom je bil v mnogih brezštevilnih množicah trirazsežnih risb, ki so občudovanja vredne.

Crennela

Za tretjo izdajo sta Kate in David Crennell popolnoma obnovila besedilo ter ponovno narisala slike in diagrame.

Pregled devetinpedesetih ikozaedrov

Pred Coxeterjem sta samo Brückner in Wheeler opazila pomembno množico stelacij, čeprav jih je bilo prej znanih zelo malo. Po izdaji dela Devetinpetdeset je Wenninger objavil navodila za izdelavo nekaterih modelov. Številčenje v tej knjigi je postalo široko uporabljano, čeprav je bilo v njem omenjenih samo nekaj stelacij.

Opombe

Števike indeksov so Crennellove, če ni drugače zapisano.

Crennell

V številčenju, ki je bilo dodano tretji izdaji, je Creenell prvih 32 oblik in zrcalnih modelov ter zadnjih 27 je kiralnih, ki imajo samo desne oblike. To je posledica reda v katerem so stelacije prikazane v knjigi.

Celice

V Du Valovi notaciji je vsaka lupina zapisana v mastnem tisku, to je a, b, c, ..., h kjer je a prvotni ikozaeder. Nekatere lupine se delijo v dve skupini celic, kot na primer e vključuje e₁ in e₂. Množica f₁ se deli še na desno-sučne in levo-sučne oblike

Stranske ploskve

Vse stelacije se lahko izrazijo s pomočjo diagrama stelacije. V diagramu, ki je prikazan, barve označujejo področja

Wheeller

Wheeller je našel obliko ikozaedra, tako, da je izbral segmente premice iz diagrama stelacije. Ločil je med Keplerjevo in klasičnim postopkom stelacije. Coxeter je s sodelavci prezrl to razliko in je obravnaval vse kot stelacije.

Brückner

Brückner je naredil in fotografiral modele mnogih poliedrov. Od njih jih je bilo bolj malo ikozaedrov.

Opombe

Številka 8 se včasih imenuje ehinaeder, ki ima ime po navidezni podobnosti s kljunatim ježkom. Ta uporaba izraza je neodvisna od Keplerjevega opisa tega pravilnega zvezdnega poliedra, ki ga on imenuje ehidna in spada v red kljunatih ježkov.

Crennell	VRML	Celice	Stranska ploskev	Wenninger	Wheeler	Brückner	Opombe
1	[1]	A	0	04 ikozaeder	1	9999 !	platonski ikozaeder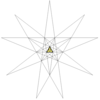
2	[2]	B	1	26 triakisni ikozaeder	2	0802 !tabela VIII, slika 2	prva stelacija ikozaedra, mali triambski ikozaeder, ali triakisikozaeder
3	[3]	C	2	23 sestav petih oktaedrov	3	0906 !tabela IX, slika 6	pravilni poliedrski sestav sestav petih oktaedrov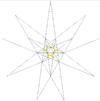
4	[4]	D	3 4	99	4	0917 !tabela IX, slika 17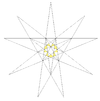
5	ikozaeder_(5)_(5_color).wrl^{[mrtva povezava]}	E	5 6 7	99	99	9999 !
6	ikozaeder_(6)_(5_color).wrl^{[mrtva povezava]}	F	8 9 10	27 druga stelacija	19	9999 !
7	stellated_icosahedron_(7)_(5_color).wrl^{[mrtva povezava]}	G	11 12	41 veliki ikozaeder	11	1124 !tabela XI, slika 24	veliki ikozaeder
8	[5]	H	13	42 končna stelacija	12	1114 !tabela XI, slika 14	končna stelacija ikozaedra ali ehinaeder
9	[6]	e₁	3' 5	37 dvanajsta stelacija	99	9999 !
10	[7]	f₁	5' 6' 9 10	99	99	9999 !
11	[8]	g₁	10' 12	29 četrta stelacija	21	9999 !
12	[9]	e₁f₁	3' 6' 9 10	99	99	9999 !
13	[10]	e₁f₁g₁	3' 6' 9 12	99	20	9999 !
14	[11]	f₁g₁	5' 6' 9 12	99	99	9999 !
15	[12]	e₂	4' 6 7	99	99	9999 !
16	[13]	f₂	7' 8	99	22	9999 !
17	[14]	g₂	8' 9' 11	99	99	9999 !
18	[15]	e₂f₂	4' 6 8	99	99	9999 !
19	[16]	e₂f₂g₂	4' 6 9' 11	99	99	9999 !
20	[17]	f₂g₂	7' 9' 11	30 peta stelacija	99	9999 !
21	[18]	De₁	4 5	32 sedma stelacija	10	9999 !
22	[19]	Ef₁	7 9 10	25 sestav desetih tetraedrov	8	0903 !tabela IX, slika 3	pravilni poliedrski sestav sestav desetih tetraedrov
23	[20]	Fg₁	8 9 12	31 šesta stelacija	17	1003 !tabela X, slika 3
24	[21]	De₁f₁	4 6' 9 10	99	99	9999 !
25	[22]	De₁f₁g₁	4 6' 9 12	99	99	9999 !
26	[23]	Ef₁g₁	7 9 12	28 tretja stelacija	9	0826 !tabela VIII, slika 26	izkopani dodekaeder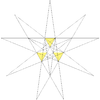
27	[24]	De₂	3 6 7	99	5	9999 !
28	[25]	Ef₂	5 6 8	99	18	0920 !tabela IX, slika 20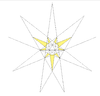
29	[26]	Fg₂	10 11	33 osma stelacija	14	9999 !
30	[27]	De₂f₂	3 6 8	34 deveta stelacija	13	9999 !	srednji triambski ikozaeder ali veliki triambski ikozaeder
31	[28]	De₂f₂g₂	3 6 9' 11	99	99	9999 !
32	[29]	Ef₂g₂	5 6 9' 11	99	99	9999 !
33	[30]	f₁	5' 6' 9 10	35 deseta stelacija	99	9999 !
34	[31]	e₁f₁	3' 5 6' 9 10	36 enajsta stelacija	99	9999 !
35	[32]	De₁f₁	4 5 6' 9 10	99	99	9999 !
36	[33]	f₁g₁	5' 6' 9 10' 12	99	99	9999 !
37	[34]	e₁f₁g₁	3' 5 6' 9 10' 12	39 štirinajsta stelacija	99	9999 !
38	[35]	De₁f₁g₁	4 5 6' 9' 10' 12	99	99	9999 !
39	[36]	f₁g₂	5' 6' 8' 9' 10 11	99	99	9999 !
40	[37]	e₁f₁g₂	3' 5 6' 8' 9' 10 11	99	99	9999 !
41	[38]	De₁f₁g₂	4 5 6' 8' 9' 10 11	99	99	9999 !
42	[39]	f₁f₂g₂	5' 6' 7' 9' 10 11	99	99	9999 !
43	[40]	e₁f₁f₂g₂	3' 5 6' 7' 9' 10 11	99	99	9999 !
44	[41]	De₁f₁f₂g₂	4 5 6' 7' 9' 10 11	99	99	9999 !
45	[42]	e₂f₁	4' 5' 6 7 9 10	40 petnajsta stelacija	99	9999 !
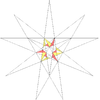
46	[43]	De₂f₁	3 5' 6 7 9 10	99	99	9999 !
47	[44]	Ef₁	5 6 7 9 10	24 sestav petih tetraedrov	7 (6: levo-sučni)	0911 !tabela IX, slika 11	pravilni poliedrski sestav sestav petih tetraedrov (desno-sučni)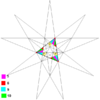
48	[45]	e₂f₁g₁	4' 5' 6 7 9 10' 12	99	99	9999 !
49	[46]	De₂f₁g₁	3 5' 6 7 9 10' 12	99	99	9999 !
50	[47]	Ef₁g₁	5 6 7 9 10' 12	99	99	9999 !
51	[48]	e₂f₁f₂	4' 5' 6 8 9 10	38 trinajsta stelacija	99	9999 !
52	[49]	De₂f₁f₂	3 5' 6 8 9 10	99	99	9999 !
53	[50]	Ef₁f₂	5 6 8 9 10	99	15 (16: levo-sučni)	9999 !
54	[51]	e₂f₁f₂g₁	4' 5' 6 8 9 10' 12	99	99	9999 !
55	[52]	De₂f₁f₂g₁	3 5' 6 8 9 10' 12	99	99	9999 !
56	[53]	Ef₁f₂g₁	5 6 8 9 10' 12	99	99	9999 !
57	[54]	e₂f₁f₂g₂	4' 5' 6 9' 10 11	99	99	9999 !
58	[55]	De₂f₁f₂g₂	3 5' 6 9' 10 11	99	99	9999 !
59	[56]	Ef₁f₂g₂	5 6 9' 10 11	99	99	9999 !