Uniformno tlakovanje
Uniformno tlakovanje je v geometriji vrsta teselacije ravnine s stranskimi ploskvami pravilnega mnogokotnika (uniformni polieder ima pravilne mnogokotnike kot stranske ploskve) z edino omejitvijo, da so ogliščnouniformni.
Uniformno tlakovanje je možno v evklidski in hiperbolični ravnini.
Večino uniformnih tlakovanj se lahko izdela s pomočjo Wythoffove konstrukcije tako, da se prične z grupo simetrije in posamezno generatorsko točko znotraj osnovne domene. Ravninska grupa simetrije ima mnogokotniško osnovno domeno in se jo lahko predstavi z zaporedjem zrcal v zaporednih ogliščih.
Osnovna domena trikotnika je (p q r) kjer so p, q in r cela števila, večja od 1, ter pravokotni trikotnik (p q 2). Trikotnik lahko obstaja kot sferni trikotnik, evklidski ravninski trikotnik ali hiperbolični ravninski trikotnik, kar je odvisno od vrednosti p, q in r.
Obstaja več simboličnih shem za imenovanje teh oblik.
Coxeterjeve grupe
[uredi | uredi kodo]| orbiterična simetrija |
Coxeterjeva grupa | Coxeter-Dinkinov diagram |
opombe | ||
|---|---|---|---|---|---|
| kompaktne | |||||
| *333 | (3 3 3) | [Δ] | 3 zrcalne oblike, 1 prirezana oblika | ||
| *442 | (4 4 2) | [4,4] | 5 zrcalnih oblik, 1 prirezana oblika | ||
| *632 | (6 3 2) | [6,3] | 7 zrcalnih oblik, 1 prirezana oblika | ||
| *2222 | (∞ 2 ∞ 2) | × | [∞] × [∞] | 3 zrcalne oblike, 1 prirezana oblika | |
| nekompaktne (frizijske) | |||||
| *∞∞ | (∞) | [∞] | |||
| *22∞ | (2 2 ∞) | × | [∞] × [ ] | 2 zrcalni obliki, 1 prirezana oblika | |
| orbiterična simetrija |
Coxeterjeva grupa | Coxeter-Dinkinov diagram |
opombe | |
|---|---|---|---|---|
| kompaktne | ||||
| *pq2 | (p q 2) | [p,q] | 2p+2q < pq | |
| *pqr | (p q r) | pq+pr+qr < pqr | ||
| parakompaktne | ||||
| *∞p2 | (p ∞ 2) | [p,∞] | p>=3 | |
| *∞pq | (p q ∞) | p,q>=3, p+q>6 | ||
| *∞∞p | (p ∞ ∞) | p>=3 | ||
| *∞∞∞ | (∞ ∞ ∞) | |||
Uniformno tlakovanje evklidske ravnine
[uredi | uredi kodo]- Za podrobne podatke o tej temi glej tlakovanje s pravilnimi mnogokotniki.
Obstajajo grupe simetrije na evklidski ravnini, ki se jo konstruira iz osnovnih trikotnikov (4 4 2) in (3 3 3). Vsakega se lahko prikaže kot množico črt odboja, ki deli ravnino v osnovne trikotnike.
Ta simetrija ustvarja tri pravilna tlakovanja in sedem polpravilnih. Številna polpravilna tlakovanja so ponovitve z različnimi konstruktorji.
Prizmatična grupa simetrije, ki je predstavljena z (2 2 2 2) pomeni skupino dveh vzporednih zrcal, ki imata v splošnem pravokotno osnovno domeno.
Naslednja prizemska grupa simetrije, ki jo predstavlja (∞ 2 2) in ima neskončno osnovno domeno. Konstruira dve uniformni tlakovanji apeirogonsko prizmo in apeirogonsko antiprizmo.
Osnovni trikotniki so pravokotni trikotniki: (p q 2)
| (p q 2) | osnovni trikotniki |
starševsko | prisekano | rektificirano | dvojnoprisekano | dvojnorektificirano (dual) |
kantelirano | omniprisekano (kantiprisekano) |
prirezana oblika |
|---|---|---|---|---|---|---|---|---|---|
| Wythoffov simbol | q | p 2 | 2 q | p | 2 | p q | 2 p | q | p | q 2 | p q | 2 | p q 2 | | | p q 2 | |
| Schläflijev simbol | t{p,q} | t{p,q} | r{p,q} | 2t{p,q}=t{q,p} | 2r{p,q}={q,p} | rr{p,q} | tr{p,q} | sr{p,q} | |
| Coxeter-Dinkinov diagram | |||||||||
| konfiguracija oglišč | pq | (q.2p.2p) | (p.q.p.q) | (p.2q.2q) | qp | (p.4.q.4) | (4.2p.2q) | (3.3.p.3.q) | |
| kvadratno tlakovanje (4 4 2) |
 V4.8.8 |
 {4,4} |
 4.8.8 |
 4.4.4.4 |
 4.8.8 |
 {4,4} |
 4.4.4.4 |
 4.8.8 |
 3.3.4.3.4 |
| šestkotno tlakovanje (6 3 2) |
 V4.6.12 |
 {6,3} |
 3.12.12 |
 3.6.3.6 |
 6.6.6 |
 {3,6} |
 3.4.6.4 |
 4.6.12 |
 3.3.3.3.6 |
Splošni osnovni trikotniki: (p q r)
| Wythoffov simbol (p q r) |
osnovni trikotniki |
q | p r | r q | p | r | p q | r p | q | p | q r | p q | r | p q r | | | p q r |
|---|---|---|---|---|---|---|---|---|---|
| Coxeter-Dinkinov diagram | |||||||||
| konfiguracija oglišč | (p.q)r | (r.2p.q.2p) | (p.r)q | (q.2r.p.2r) | (q.r)p | (q.2r.p.2r) | (r.2q.p.2q) | (3.r.3.q.3.p) | |
| trikotniško tlakovanje (3 3 3) |
 V6.6.6 |
 (3.3)3 |
 3.6.3.6 |
 (3.3)3 |
 3.6.3.6 |
 (3.3)3 |
 3.6.3.6 |
 6.6.6 |
 3.3.3.3.3.3 |
Uniformna tlakovanja hiperbolične ravnine
[uredi | uredi kodo]Znanih je neskončno veliko uniformnih tlakovanj s konveksnimi mnogokotniki v [[hiperbolična ravnina|hiperbolični ravnini. Vsako tlakovanje je osnovano na drugi grupi zrcalne simetrije (p q r).
Pravokotni osnovni trikotniki: (p q 2)
| (p q 2) | osnovni trikotniki |
starševsko | prisekano | rektificirano | dvojnoprisekano | dvojnorektificirano (dualno) |
kantelirano | omniprisekano (kantiprisekano) |
prirezana oblika |
|---|---|---|---|---|---|---|---|---|---|
| Wythoffov simbol | q | p 2 | 2 q | p | 2 | p q | 2 p | q | p | q 2 | p q | 2 | p q 2 | | | p q 2 | |
| Schläflijev simbol | t{p,q} | t{p,q} | r{p,q} | 2t{p,q}=t{q,p} | 2r{p,q}={q,p} | rr{p,q} | tr{p,q} | sr{p,q} | |
| Coxeter-Dinkinov diagram | |||||||||
| konfiguracija oglišč | pq | (q.2p.2p) | (p.q.p.q) | (p.2q.2q) | qp | (p.4.q.4) | (4.2'p.2q') | (3.3.p.3.q) | |
| (hiperbolična ravnina) (5 4 2) |

|
 {5,4} |
 4.10.10 |
 4.5.4.5 |
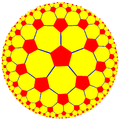 5.8.8 |
 {4,5} |
 4.4.5.4 |
 4.8.10 |
 3.3.4.3.5 |
| (hiperbolična ravnina) (5 5 2) |

|
 {5,5} |
 5.10.10 |
 5.5.5.5 |
 5.10.10 |
 {5,5} |
 5.4.5.4 |
 4.10.10 |
 3.3.5.3.5 |
| (hiperbolična ravnina) (7 3 2) |

|
 {7,3} |
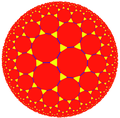 3.14.14 |
 3.7.3.7 |
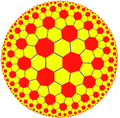 7.6.6 |
 {3,7} |
 3.4.7.4 |
 4.6.14 |
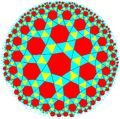 3.3.3.3.7 |
| (hiperbolična ravnina) (8 3 2) |

|
 {8,3} |
 3.16.16 |
 3.8.3.8 |
 8.6.6 |
 {3,8} |
 3.4.8.4 |
 4.6.16 |
 3.3.3.3.8 |
Splošni osnovni trikotniki (p q r)
| Wythoffov simbol (p q r) |
osnovni trikotniki |
q | p r | r q | p | r | p q | r p | q | p | q r | p q | r | p q r | | | p q r |
|---|---|---|---|---|---|---|---|---|---|
| Coxeter-Dinkinov diagram | |||||||||
| konfiguracija oglišč | (p.r)q | (r.2p.q.2p) | (p.q)r | (q.2r.p.2r) | (q.r)p | (q.2r.p.2r) | (r.2q.p.2q) | (3.r.3.q.3.p) | |
| hiperbolična (4 3 3) |

|
 (3.4)3 |
 3.8.3.8 |
 (3.4)3 |
 3.6.4.6 |
 (3.3)4 |
 3.6.4.6 |
 6.6.8 |
 3.3.3.3.3.4 |
| hiperbolična (4 4 3) |

|
 (3.4)4 |
 3.8.4.8 |
 (4.4)3 |
 3.6.4.6 |
 (3.4)4 |
 4.6.4.6 |
 6.8.8 |
 3.3.3.4.3.4 |
| hiperbolična (4 4 4) |

|
 (4.4)4 |
 4.8.4.8 |
 (4.4)4 |
 4.8.4.8 |
 (4.4)4 |
 4.8.4.8 |
 8.8.8 |
Slika:Uniform tiling 444-snub.svg 3.4.3.4.3.4 |
Sebidualna tlakovanja
[uredi | uredi kodo]Tlakovanje je lahko tudi sebidualno. Takšno je kvadratno tlakovanje s Schläflijevim simbolom {4,4}.
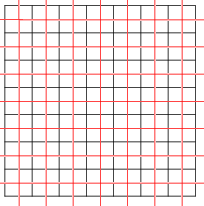 Kvadratno tlakovanje (črno) {4,4} s svojim dualnim tlakovanjem (rdeče). |
Glej tudi
[uredi | uredi kodo]- Wythoffov simbol
- seznam uniformnih tlakovanj
- uniformna tlakovanja v hiperbolični ravnini
- uniformni politop
Zunanje povezave
[uredi | uredi kodo]- Weisstein, Eric Wolfgang. »Uniform Tessellation«. MathWorld.
- Uniformne teselacije v evklidski ravnini (angleško)
- Teselacije v ravnini (angleško)
- Svet teselacij Davida Baileya (angleško)
- k-uniformna tlakovanja Arhivirano 2006-09-09 na Wayback Machine. (angleško)
- n-uniformna tlakovanja (angleško)
- Evklidske teselacije (angleško)




